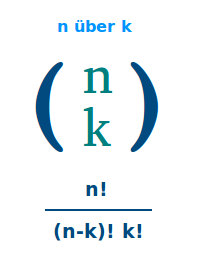n über k
n!/[(n-k)!k!]
5 über 3 gibt ausgerechnet 10: man nennt den ganzen Ausdruck den Binomialkoeffizienten. Wichtig ist er in der Stochastik und Kombinatorik und steht im Zusammenhang mit dem Pascalschen Dreieck. Hier ist die Berechnung kurz erklärt. => Ganzen Artikel lesen …
Mathematik | Physik | Chemie
Das kleine und lateinische n und das große lateinische N stehen oft Anzahlen, also Dinge, die man durch Zählen bestimmen kann. Es gibt aber auch andere Bedeutungen. Hier steht eine Überschrift. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Übersicht
K für Kelvin und k für Kilo: das große und das kleine lateinische K haben in der Mathematik und den Wissenschaften verschiedene Bedetungen. Einige wichtige davon sind hier kurz aufgelistet. => Ganzen Artikel lesen …
… ist per Definition immer 1, mehr unter => Binomialkoeffizient
… ist per Definition genau 1. Mehr unter => n über k
… ist genau 1. Mehr unter => n über k
Teekessel
Das Spielzeug ist hinüber (kaputt) oder: man geht zu einer Freundin hinüber und meint damit vielleicht die andere Straßenseite. Das Wort hinüber hat also zwei Bedeutungen und ist damit ein => Teekessel
Rechtschreibung
„Sie sprang laut schreiend übers Bächlein.“ ist korrekt. Siehe auch => unters
Ableiten über Kettenregel
Analysis
Die Funktion f(x)=(4x+2)³ gibt abgeleitet 4·3·(4x+2)². Die verwendete Regel war als Merkspruch: innere Ableitung (das gab hier die Zahl 4) mal äußerer Ableitung (das gab das 3·(4x+2)². Das wird hier kurz vorgestellt. => Ganzen Artikel lesen …
Substitution
Eine Funktion der Form f(g(x)) nennt man verkettet: der Funktionswert der inneren Funktion wird als Argument in die äußere Funktion eingesetzt. Die Stammfunktion (Aufleitung) einer solchen Funktion kann man oft - aber nicht immer - bestimmen über eine Substitution. Lies mehr unter => Integrieren über Substitution
… e hoch x²+4x gibt abgeleitet e hoch x²+4c und das ganze mal 2x plug 4, mehr unter => e-Funktion ableiten
Anleitung
Man hat zwei Punkte in einem Koordinatensystem gegeben. Hier wird kurz erklärt, wie man die Mitte berechnet und wie sie definiert ist. => Ganzen Artikel lesen …
… siehe unter => Binomialkoeffizient berechnen
… für kubische oder höhere Funktionen => Satz über rationale Nullstellen
… für kubische oder höhere Funktionen => Satz über rationale Nullstellen
… für kubische oder höhere Funktionen => Satz über rationale Nullstellen
… für kubische oder höhere Funktionen => Satz über rationale Nullstellen
Methode
Man erstellt sich eine Art Katalog für verschiedene Aufgabentypen. Für jeden Aufgabentypen hat man dann einen feste Lösungsweg. Diese Methode eignet sich, wenn Fragestellungen in immer wieder ähnlichen Typen vorkommen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
