 Komplexe Zahl
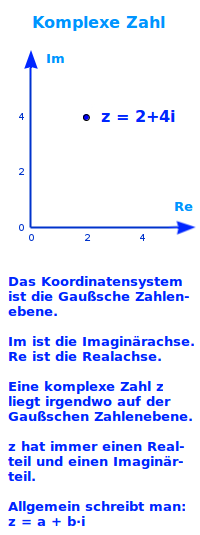
Komplexe Zahl
Definition
Komplex nennt man eine Zahl, die auch jenseits der Zahlengeraden kann (aber nicht muss). Veranschaulicht wird sie als Punkt in der sogenannten gaußschen Zahlenebene. Ein Überblick zum ganzen Thema steht unter => Rechnen mit komplexen Zahlen
 Zahl
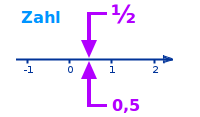
Zahl
Mathematik
Eine Zahl ist ein Begriff, das heißt eine Vorstellung, von einem Wie-Viel oder Wie-Vielen. Die Zahl selbst ist etwas anderes als ihre Darstellung. Jeder eigene Punkt auf der Zahlengerden ist eine eigene Zahl. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… oft mit großem C bezeichnet, mehr unter => Komplexe Zahl
… oft mit großem C bezeichnet, mehr unter => Komplexe Zahl
… oft mit großem C bezeichnet, mehr unter => Komplexe Zahl
Beispiele
Als komplex bezeichnet man eine Zahl, die veranschaulicht auch jenseits der Zahlengeraden liegen kann. Sie setzt sich zusammen aus einem Realteil und einem imaginären Teil. Hier folgen Beispiele. => Ganzen Artikel lesen …
… oft mit großem C bezeichnet, mehr unter => Komplexe Zahl
Mathematik
Eine anormal-komplexe Zahl z ist definiert über z = a+bj mit j²=1. Dazu ein Rechenbeispiel zur Multiplikation: (4+2j)·(5+3j) = 20 + 12j + 10j + 6j² = 26 + 22j. Die anormal-komplexe Zahl ist ein Sonderfall einer hyperkomplexen Zahl. Siehe auch => komplexe Zahl
… Schritt-für-Schritt-Erklärung unter => Fortran90 atan2
Programmieren
Einer der Gründe, warum vor allem Naturwissenschaftler gerne mit der Programmiersprache Fortran90 arbeiten ist der komfortable Umgang mit komplexen Zahlen wie zum Beispiel der Zahl (2+4i). Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Kurzes Beispielprogramm
Programm fängt an -> => Ganzen Artikel lesen …
… Schritt-für-Schritt-Erklärung unter => Fortran90 atan2
… ist nicht definiert, mehr unter => größer und kleiner bei komplexen Zahlen
… ist nicht definiert, mehr unter => größer und kleiner bei komplexen Zahlen
… ist nicht definiert, mehr unter => größer und kleiner bei komplexen Zahlen
… a+Siehe unter => Komplexe Zahl in kartesischer Form
… ist z. B. ein Quaternion, siehe unter => keine komplexen Zahlen
… ist nicht definiert, mehr unter => größer und kleiner bei komplexen Zahlen
… ist nicht definiert, mehr unter => größer und kleiner bei komplexen Zahlen
… ist nicht definiert, mehr unter => größer und kleiner bei komplexen Zahlen
… meint dasselbe wie => Komplexe Zahl in kartesischer Form
… Definition unter => Wurzel einer komplexen Zahl
… a+Siehe unter => Komplexe Zahl in kartesischer Form
Anleitung
(4+3i) durch (2+2i) gibt (1,75-0,25i): hier werden zwei Varianten vorgestellt, wie man eine komplexe Zahl durch eine weitere komplexe Zahl dividieren, also teilen, kann. => Ganzen Artikel lesen …
… Berechnung mit Beispiel unter => Gegenzahl einer komplexen Zahl
… ist nicht definiert, mehr unter => größer und kleiner bei komplexen Zahlen
… z. B. (4+2i)³ => Moivrescher Satz
… zum Potenzieren komplexer Zahlen, siehe unter => Moivrescher Satz
… zum Potenzieren komplexer Zahlen, siehe unter => Moivrescher Satz
… z. B. die Zahl 4+2i => komplexe Zahl in kartesischer Form
 Komplexe Zahl in Exponentialform
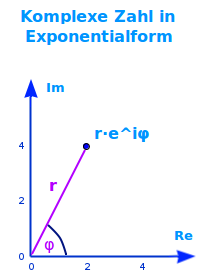
Komplexe Zahl in Exponentialform
Definition
z = r mal e hoch (i mal phi) oder kurz geschrieben als r·e^iφ ist die Exponentialform einer komplexen Zahl. Mit dieser Darstellung lassen sich vor allem gut die Multiplikation und Division durchführen. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… a+Siehe unter => Komplexe Zahl in kartesischer Form
 Komplexe Zahl in kartesischer Form
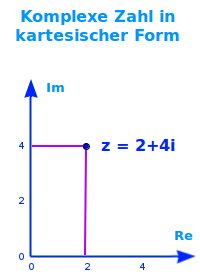
Komplexe Zahl in kartesischer Form
Definition
z = a + bi: dies ist die kartesische oder algebraische Darstellung einer komplexen Zahl. Damit lassen sich vor allem gut die Addition und Subtraktion durchführen. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… a+Siehe unter => Komplexe Zahl in kartesischer Form
… a+Siehe unter => Komplexe Zahl in kartesischer Form

