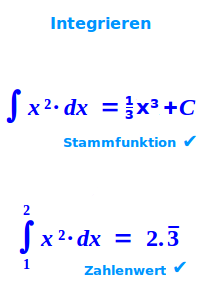Integrieren

Mathematik

Zu f(x) eine Aufleitung F(x) oder den konkreten Zahlenwert für bestimmte Grenzen dafür berechnen: beides wird oft integrieren oder auch aufleiten genannt. Hier steht eine kurze Unterscheidung der zwei Begriffe. => Ganzen Artikel lesen …

2: 0 integrieren

… gibt 0, mehr unter => 0 aufgeleitet

3: 1 integrieren

… gibt x, mehr unter => 1 aufgeleitet

4: C integrieren

… Zahl + oder - am Ende einer Aufleitung => Integrationskonstante

5: x integrieren

… ist 0,5x², mehr unter => x aufgeleitet

6: a beim Integrieren

… meint wahrscheinlich dasselbe wie => Linke Integrationsgrenze

7: a und b beim Integrieren

… stehen oft für die beiden => Integrationsgrenzen

Anschaulich integrieren

Visuell denken

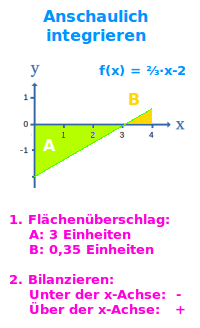
Integrieren heißt hier: den Wert eines bestimmten Integrals bestimmen. Eine überschlägige Abschätzung kann oft durch rein bildliches Denken bestimmt werden. Das wird hier an einem Beispiel Schritt-für-Schritt kurz erklärt. => Ganzen Artikel lesen …

9: b beim Integrieren

… meint wahrscheinlich dasselbe wie => Rechte Integrationsgrenze

10: cosinus integrieren

… gibt sin(Siehe unter => cosinus x aufgeleitet

11: cosinus x integrieren

… gibt sin(Siehe unter => cosinus x aufgeleitet

12: e hoch integrieren

… ist e hoch x, mehr unter => e hoch x aufgeleitet

13: e hoch x integrieren

… ist e hoch x, mehr unter => e hoch x aufgeleitet

14: Eine 0 integrieren

… gibt 0, mehr unter => 0 aufgeleitet

15: Eine 1 integrieren

… gibt x, mehr unter => 1 aufgeleitet

16: Eine cosinus x integrieren

… gibt sin(Siehe unter => cosinus x aufgeleitet

17: Eine e hoch x integrieren

… ist e hoch x, mehr unter => e hoch x aufgeleitet

18: Eine Eins integrieren

… gibt x, mehr unter => 1 aufgeleitet

19: Eine Null integrieren

… gibt 0, mehr unter => 0 aufgeleitet

20: Eine sinus x integrieren

… -cos(Siehe unter => sinus x aufgeleitet

21: Eine Wurzel integrieren

… (2/3)x^1,5, mehr unter => Wurzel aufgeleitet

22: Eine x integrieren

… ist 0,5x², mehr unter => x aufgeleitet

23: Eine Zahl integrieren

… ist immer Zahl mal x, mehr unter => Zahl aufgeleitet

24: Eins integrieren

… gibt x, mehr unter => 1 aufgeleitet

25: Faktoren Integrieren

… steht unter => Partiell integrieren

26: Faktoren von x integrieren

… steht unter => Partiell integrieren

27: Flächen berechnen integrieren

… über Integrieren, siehe unter => Fläche unter der Kurve berechnen

28: Flächen berechnen über Integrieren

… über Integrieren, siehe unter => Fläche unter der Kurve berechnen

29: Flächenberechnung Integrieren

… über Integrieren, siehe unter => Fläche unter der Kurve berechnen

31: Grenzen beim Integrieren

… oft a und b genannt, siehe unter => Integrationsgrenzen

32: Integration über partielles Integrieren

… siehe unter => Integrieren über partielle Integration

33: Integrieren mit u und v

… Erklärung mit Beispiel unter => Partiell integrieren

34: Integrieren mit v und u.Integration mit v und u

… Erklärung mit Beispiel unter => Partiell integrieren

35: Integrieren über partielle Integration

… mit u und v oder g(x) und f(Siehe unter => Partielle Integration