… z. B.: 3/4 und 24/32
Brüche sind dann genau dann gleichwertig, sie gekürzt dasselbe ergeben. Sie sind auch gleichwertig, wenn sie dieselbe Dezimalzahl ergeben. Diese und auch andere Methoden werden hier kurz vorgestellt. => Ganzen Artikel lesen …
 Brüche
Brüche
Beispiele, Arten
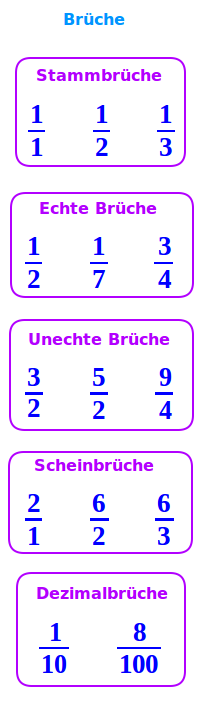
½, ⅘, ⅞: als Bruch bezeichnet man eine Zahl, die mit einem Bruchstrich in Bruchform geschrieben ist. Hier folgen verschiedene Arten von Brüchen (Stammbruch, echter Bruch etc.) sowie einzelne Beispiele mit Namen. => Ganzen Artikel lesen …
… mehrere Methoden unter => gleichwertige Brüche erkennen
… Beispiel 4/10 und 2/5 sind gleichwertig
Zwei Brüche sind gleichwertig, wenn sie gleich viel meinen. Kürzt man beide Brüche so weit wie möglich, haben sie am Ende denselben Zähler und Nenner. In eine Dezimalzahl umgerechnet ergeben sie beide dieselbe Zahl. => Ganzen Artikel lesen …
Anleitung
3/4 + 2/5 = 5/4: gleichnamig heißt, dass die Nenner (unten) unten gleich sind. Die Nenner benennen die Brüche, geben ihnen also ihren Namen, hier sind es: Viertel. Wenn die Nenner gleich sind muss man nur die Zähler addieren. Das ist hier mit Zahlenbeispielen kurz erklärt. => Ganzen Artikel lesen …

