Verfahren geht immer
20 hat die Teilerliste {1,2,4,5,10,20} und 25 hat die Teilerliste {1,3,5,15}. Die größte Zahl in beiden Teilerlisten ist die 5. Also ist die 5 der größte gemeinsame Teiler, kurz der ggT. Das wird hier weiter erklärt. => Ganzen Artikel lesen …
 ggT
ggT
Definition
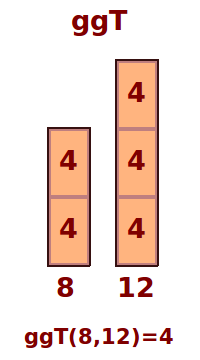
In der Mathematik ist der ggT der größte gemeinsame Teiler von zwei Zahlen. Die Schreibweise ggT(8,12) = 4 heißt, dass die Zahlen 8 und 12 als größten gemeinsamen Teiler die Zahl 4 haben. Das ist hier erklärt. => Ganzen Artikel lesen …
 Über
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Anleitung
Gesucht ist der größte gemeinsame Teiler von zwei gegebenen Zahlen. Es gibt ein Verfahren, dass immer mit denselben Schritten zum Ziel führt. Solche Verfahren nennt man auch einen Algorithmus. Für diesen Algorithmus hier muss man schon mit Potenzen rechnen können. Das Verfahren ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Anleitung
Die Drei hat als Vielfache die Zahlen: 0, 3, 6, 9, 12, 15 und so weiter. Die Vier hat als Vielfache die Zahlen: 0, 4, 8, 12, 16 und so weiter. Die kleinste Zahl, die von beiden ein Vielfaches ist, ist hier die 12. Man schreibt: kgV(3;4)=12. Das Verfahren zur Bestimmung über Zahlenreihen ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Teilermenge
T = {1,2,3,6,9,18} ist die Teilerliste für die Zahl 18. Man benennt die Liste oft mit einem großen T. In geschweiften Klammern stehen dann von klein nach groß alle Teiler einer Zahl. Die 1 ist immer die erste Zahl in der Zahl. Die Zahl, für die die Teiler bestimmt werden ist immer die letzte Zahl in der Liste. Die Teilerliste ist dasselbe wie die => Teilermenge
… Mm Sinne von Vorzahlen, siehe unter => Koeffizienten
Reibungsbeiwert, Ausdehnungsbeiwert etc.: statt Beiwert sagt man auch Koeffizient, siehe unter => Koeffizienten

