Gerade Zahlen

Alle Zahlen aus der Zweierreihe, zum Beispiel…

0 - 2 - 4 - 6 - 8 - 10 - 12 - 14 - 16 und so weiter => Ganzen Artikel lesen …

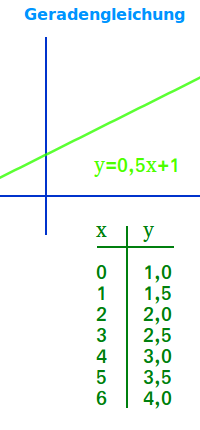
Gerade

Übersicht

Eine Gerade in der Mathematik ist eine Linie ohne Ecken, Lücken, Kurven oder Enden: sie ist unendlich lang gedacht. Die kürzeste Verbindung zwischen zwei Punkten liegt immer auf einer Geraden. Hier werden Geraden in verschiedenen Teilgebieten der Mathematik kurz vorgestellt. => Ganzen Artikel lesen …

3: Zahlen

… Brüche, Dezimalzahlen, Kommazahlen etc. => Zahlenarten

4: Grade Zahlen

… siehe unter => gerade Zahlen

Ungerade Zahlen

Beispiele

1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 sind alle ungerade. Aber auch negative Zahlen können ungerade sein: -17 -15 -13 -11 -9 -7 -5 -3 -1. Zur Definition siehe unter => ungerade Zahl

7: Zwei gerade Zahlen addiert

… ergeben immer wieder eine gerade Zahl, Beispiel: 8+4=12. Siehe auch => gerade Zahl

8: Zwei gerade Zahlen malrechnen

… gibt immer eine gerade Zahl, Beispiel: 4·12=48. Siehe auch => gerade mal gerade

9: Zwei gerade Zahlen multiplizieren

… gibt immer eine gerade Zahl, Beispiel: 8·10=80. Mehr unter => gerade mal gerade

10: Zwei gerade Zahlen plusrechnen

… gibt immer wieder eine gerade Zahl, z. B. 8+4=12. Mehr unter => gerade plus gerade

11: Zwei ungerade Zahlen addieren

… gibt immer eine gerade Zahl, Beispiel: 5+3=8, siehe auch => ungerade plus ungerade

12: Zwei ungerade Zahlen malrechnen

… gibt immer eine ungerade Zahl, Beispiel: 3·9=27, mehr unter => ungerade mal ungerade

14: Zwei ungerade Zahlen plusrechnen

… gibt immer eine gerade Zahl, Beispiel: 5+3=8, mehr unter => ungerade plus ungerade