f'(x) = 0
Man hat hat eine Funktion f(x) und leitet sie einmal ab. Diese erste Ableitung nennt man auch f'(x). Diese erste Ableitung gleich null setzten heißt, man sucht einen x-Wert, bei dem für f'(x) die Zahl 0 herauskommt. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Ganz am Anfang
In der Zahl 320 ist die erste Ziffer eine 3. „Die erste“ gibt hier die Position innerhalb einer Rangfolge an. Sie hat damit mathematisch gesehen die Rolle einer => Ordinalzahl
 Ableitung
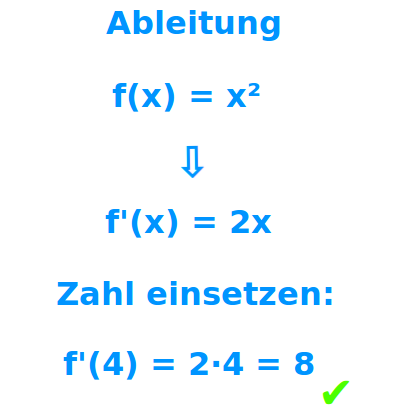
Ableitung
f'(x)
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
Bedeutungen
Gleich regnet es es; oder: das Gewicht der Tomaten und der Erbsen ist gleich: hier werden zwei Bedeutungen des Wortes kurz vorgestellt. => Ganzen Artikel lesen …
Als Zahl
Die Null ist eine eigene Zahl und steht für „nichts“ oder eine „leere Menge“. Die Null ist eine reelle, eine rationale, eine ganze und eine gerade Zahl. Sie ist keine Prinmzahl, sie ist nicht natürlich und weder negativ noch positiv. Hier stehen einige Rechenregeln rund um die Null. => Ganzen Artikel lesen …
… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
Möglichkeiten
f'''(x) = 0, also die dritte Ableitung von f(x) ist an einer Stelle null. Das eröffnet mehrere mögliche Interpretationen für den Graphen. => Ganzen Artikel lesen …
… Bedeutungen unter => erste Ableitung gleich null
Anschaulich
f''(x) = 0, also die zweite Ableitung von f(x) ist an einer Stelle null: diese Information alleine lässt so gut wie keinen weiteren Schluss auf die Form des Graphen zu. Möglich ist, dass der Graph an dieser Stelle einen Hoch- oder Tief-, Sattel- oder Wendepunkt hat oder dass er dort eine Gerade ist. Die Möglichkeiten sind hier kurz vorgestellt. => Ganzen Artikel lesen …

