Methoden
12:4 und 2:0,5 kann man beides anschaulich rechnen. Bei der ersten Aufgabe ist das Ergebnis 3 und bei der zweiten Aufgabe ist es 4. Hier sind verschiedene Methoden kurz vorgestellt. => Ganzen Artikel lesen …
Anschaulich
Mit einem Denkbild
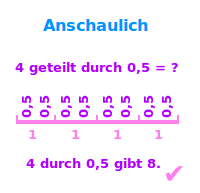
So, dass visuell-grapisches Denken mit einbezogen wird. Beispiel: was gibt 4 geteilt durch 0,5? Man kann die Aufgabe formal-rechnerisch, indem man sie z. B. als Bruch schreibt 4/0,5 dann erweitert 40/5 und am Ende den Wert berechnet, hier also 8. Als Alternative zur formalen Lösung wird hier ein anschaulicher Weg gezeigt. Lies mehr unter => anschaulich rechnen
Teilen
Grundschule
Das Teilen, wie etwa 8 durch 4 kann auf verschiedene Weisen gelöst werden. Hier werden zwei anschauliche und einige mehr rechnerische Verfahren vorgestellt. => Ganzen Artikel lesen …
Analysis
Anschaulich ableiten kann einmal heißen: man betrachtet einen Graphen von f(x) und bestimmt daraus qualitativ den Graphen der Ableitungsfunktion f'(x). Anschaulich ableiten kann aber auch heißen, dass man eine bildliche Bedeutung des Verfahrens nutzt. Verschiedene Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Anschaulich rechnen
Anleitungen
Man unterscheidet anschauliches und formales rechnen. Wer formal rechnet folgt dabei Regeln ohne dass ein erkennbarer Bezug zu Größen, Längen oder Mengen nötig ist. Beim anschaulichen Rechnen hingegen stehen sinnlich wahrnehmbare Dinge im Mittelpunkt. Hier stehen einige Tipps dazu. => Ganzen Artikel lesen …
Anschaulich integrieren
Visuell denken
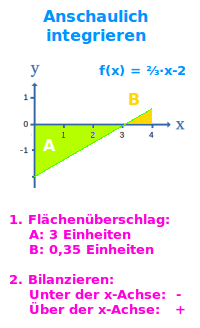
Integrieren heißt hier: den Wert eines bestimmten Integrals bestimmen. Eine überschlägige Abschätzung kann oft durch rein bildliches Denken bestimmt werden. Das wird hier an einem Beispiel Schritt-für-Schritt kurz erklärt. => Ganzen Artikel lesen …
Veranschaulichen
Methoden
Etwas veranschaulichen, man sagt auch visualisieren, heißt, sich ein inneres Bild von etwa machen. Ein gute Veranschaulichung liefert für viele Rechen- und Mathematik-Aufgaben oft gute Lösungsideen. Hier stehen einige Möglichkeiten, etwas zu veranschaulichen. => Ganzen Artikel lesen …
