Anschaulich integrieren
Visuell denken
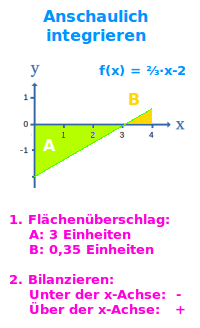
Integrieren heißt hier: den Wert eines bestimmten Integrals bestimmen. Eine überschlägige Abschätzung kann oft durch rein bildliches Denken bestimmt werden. Das wird hier an einem Beispiel Schritt-für-Schritt kurz erklärt. => Ganzen Artikel lesen …
Anschaulich
Mit einem Denkbild
So, dass visuell-grapisches Denken mit einbezogen wird. Beispiel: was gibt 4 geteilt durch 0,5? Man kann die Aufgabe formal-rechnerisch, indem man sie z. B. als Bruch schreibt 4/0,5 dann erweitert 40/5 und am Ende den Wert berechnet, hier also 8. Als Alternative zur formalen Lösung wird hier ein anschaulicher Weg gezeigt. Lies mehr unter => anschaulich rechnen
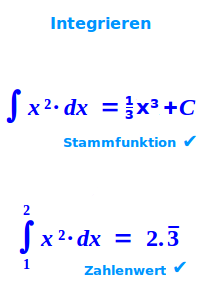Integrieren
Mathematik
Zu f(x) eine Aufleitung F(x) oder den konkreten Zahlenwert für bestimmte Grenzen dafür berechnen: beides wird oft integrieren oder auch aufleiten genannt. Hier steht eine kurze Unterscheidung der zwei Begriffe. => Ganzen Artikel lesen …
… siehe unter => anschaulich teilen
Methoden
12:4 und 2:0,5 kann man beides anschaulich rechnen. Bei der ersten Aufgabe ist das Ergebnis 3 und bei der zweiten Aufgabe ist es 4. Hier sind verschiedene Methoden kurz vorgestellt. => Ganzen Artikel lesen …
Analysis
Anschaulich ableiten kann einmal heißen: man betrachtet einen Graphen von f(x) und bestimmt daraus qualitativ den Graphen der Ableitungsfunktion f'(x). Anschaulich ableiten kann aber auch heißen, dass man eine bildliche Bedeutung des Verfahrens nutzt. Verschiedene Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Beispiele
Das Verbalisieren (Versprachlichen) von Rechenaufgaben übersetzt die Symbole und Zahlen oft in halbanschauliche Begriffe. Damit springen oft einfache und schnelle Lösungswege ins Auge. Lies mehr dazu unter => anschaulich rechnen
