Allgemeines Viereck
Ein Viereck ohne besondere Eigenschaften
Allgemein heißt in der Mathematik so viel wie „jedes“, „irgendeines“. Jedes Viereck gehört zu den allgemeinen Vierecken. Bei einem allgemeinen Viereck ist es egal, wie lang die Seiten sind, welche Innenwinkel es gibt oder ob Seiten zueinander parallel sind. Wenn es heißt „zeichne ein allgemeines Viereck“, dann zeichnet man am besten ein schiefes Viereck mit unterschiedlich langen Seiten. Siehe auch => Vierecksarten
Viereck
Eine flache Figur mit genau vier Ecken und vier geraden Seiten
Ein Viereck ist immer flach (2D), hat genau vier Ecken und nur geraden Verbindungsstrecken. Siehe auch unter => Viereck erkennen
Irgendein Dreieck, egal wie
Meint man irgendein Dreieck und ist es egal ob irgendwelche Seiten gleich lang sind oder irgendwelche Winkel gleich groß oder irgendeine Symmetrie gilt, dann sagt man: allgemeines Dreieck. Eine Formel, die also für ein allgemeines Dreieck gilt, gilt damit automatisch für jedes Dreieck. Siehe auch => Standarddreieck
Funktionen, z. B. f(x) = ax³-2x²+4x-1
Funktionen kann man durch (erlaubte) Äquivalenzumformungen in unendlich vielen Darstelungsformen bringen. f(x) = 4x+3 kann man auch schreiben als f(x) = 3+4x oder als f(x) = 4x+5-2. Als allgemeine bezeichnet man einen festen Bauplan der für jeden Funktionstyp genau festgelegt ist. Beispiele stehen unter => Allgemeine Formen
Beispiele für etwas wie: f(x) = ax²+bx+c
Zur Klassifizierung von Funktionen benutzt man sogenannte allgemeine Formen. Kann man eine gegebene Funktionslgeichung durch Äquivalenzumformen in diese Form bringen, dann gehört sie zum entsprechenden Typ. Hier stehen einige häufig genannte Typen => Ganzen Artikel lesen …
… gegenüberliegende Seiten sind parallel => Parallelogramm
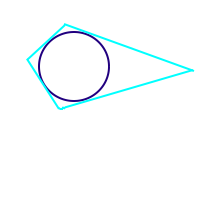Tangentenviereck
Definition
Ein Viereck, in das man innen einen sogenannten Inkreis zeichnen kann ist ein Tangentenviereck. Der Inkreis muss jede Seite des Vierecks genau einmal berühren, aber nicht schneiden. Jede Seite des Vierecks ist dann eine Tangente des Kreises. Das it hier ausführlich erklärt. => Ganzen Artikel lesen …
