 Zweite Ableitung
Zweite Ableitung
f''(x)
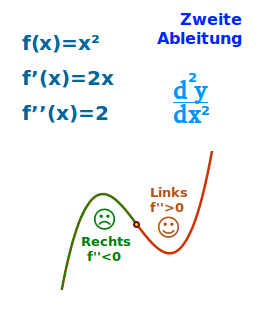
f(x)=2x³ einmal abgeleitet gibt f'(x)=6x². Das noch einmal abgeleitet gibt f''(x)=12x. Das ist die zweite Ableitung f''(x) der ursprünglichen Funktion. Die zweite Ableitung hilft zu entscheiden, wo der Graph von f(x) links- und wo er rechtsgekrümmt ist. Zudem hilft sie zu entscheiden, welche Art von Extrempunkt (Hoch- oder Tiefpunkt?) vorliegt. Beide Themen sind hier näher erklärt. => Ganzen Artikel lesen …
Mathematisch
In dem Wort TAU ist der Buchstabe A der zweite Buchstabe. Und in einer neuen Woche ist der Dienstag der zweite Tag. Der erste Tag ist der Montag. Man spricht von einer sogenannten Ordinal- oder Ordnungszahl. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
 Ableitung
Ableitung
f'(x)
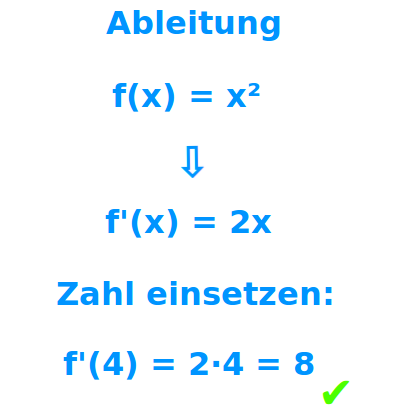
Die Ableitung steht einmal für die Steigung (als Zahl) an einem bestimmten Punkt auf einem Funktionsgraphen. Präziser spricht man hier auch vom Ableitungswert. Als Ableitung bezeichnet man auch eine Funktion f'(x), die für jeden x-Wert die dort geltende Steigung am Graphen angibt.[1][2] Präziser wäre hier: Ableitungsfunktion => Ganzen Artikel lesen …
Besser: Ableitung nach der Zeit
Zeitableitung heißt, dass man eine Funktion f(x) hat und das x für einen Zeitpunkt steht. Die Ableitung ergibt f'(x) oder dy/dt (dx=dt). In Sachkontexten ist die Ableitung nach der Zeit immer eine => momentane Änderungsrate
Beispiele
f(x) = x³ einmal abgeleitet gibt f'(x) = 3x². Das dann noch einmal abgleitet gibt f''(x) = 6x¹. Dazu stehen hier noch einige Beispiele. => Ganzen Artikel lesen …
… wie x² zu Siehe unter => erste Ableitung bilden
… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
… meint, sie wird = 0: siehe unter => zweite Ableitung gleich null
… siehe unter => Krümmung berechnen
… siehe unter => Krümmung berechnen
… siehe unter => Krümmung berechnen
… kann mehrere Dinge bedeuten => Zweite Ableitung gleich null
… wie x² zu 2, mehr unter => zweite Ableitung bilden
… siehe unter => Zweite Ableitung bilden
… siehe unter => Zweite Ableitung bilden
Beispiele
f'(x) noch einmal abgeleitet ergibt die zweite Ableitung f''(x). Dazu stehen hier einige Beispiele. => Ganzen Artikel lesen …
… wie x² zu 2, mehr unter => zweite Ableitung bilden
… siehe unter => Zweite Ableitung bilden
… was das bedeutet unter => zweite Ableitung gleich null
… was das bedeutet unter => zweite Ableitung gleich null
… was das bedeutet unter => zweite Ableitung gleich null
Anschaulich
f''(x) = 0, also die zweite Ableitung von f(x) ist an einer Stelle null: diese Information alleine lässt so gut wie keinen weiteren Schluss auf die Form des Graphen zu. Möglich ist, dass der Graph an dieser Stelle einen Hoch- oder Tief-, Sattel- oder Wendepunkt hat oder dass er dort eine Gerade ist. Die Möglichkeiten sind hier kurz vorgestellt. => Ganzen Artikel lesen …
… was das bedeutet unter => zweite Ableitung gleich null
… was das bedeutet unter => zweite Ableitung gleich null
… siehe unter => Krümmung berechnen
ẍ steht in der Physik für die Geschwindigkeit
Die Beschleunigung ist die zweite Ableitung f''(x) der Strecke nach der Zeit. Mit anderen Worten: in einem xy-Graphen, bei die x-Achse für eine Zeit und die y-Achse für eine zurückgelegte Strecke steht, gibt die erste Ableitung die Geschwindigkeit und die zweite Ableitung f''(x) gibt die Beschleunigung zur Zeit x. => Ganzen Artikel lesen …
… siehe unter => Krümmung berechnen
… was das bedeutet unter => zweite Ableitung gleich null
… was das bedeutet unter => zweite Ableitung gleich null
… was das bedeutet unter => zweite Ableitung gleich null
… gibt die Krümmung, alles Weitere unter => Zweite Ableitung

