Zuordnung
Erklärung | Beispiel
Alles was man sinnvoll in einer Tabelle aus zwei Spalten darstellen könnte. Man kann zum Beispiel Ländern bestimmte Tierarten zuordnen, die dort heimisch sein. Eine Zuordnung kann - muss aber nicht - mit einer Rechenformel in Verbindung stehen. => Ganzen Artikel lesen …
Mathematik | Physik
Der Begriff Ordnung bezeichnet in der Mathematik oft eine Stellung innerhalb einer Rangfolge. In der Physik steht er für erkennbare Strukturen und Muster. In der Theorie der Wissenschaft an sich ist eine => Ganzen Artikel lesen …
… in der Mathematik => Zuordnung
Begriffsklärung
Die Lebenserwartung von Stubenfliegen liegt um die 20 Tage, von Goldhamstern bei etwa 3 Jahren, bei Elefanten um die 60 Jahre und bei Menschen um die 80. Man kann sagen: jeder Tierart ist eine bestimmte Lebenserwartung zugeordnet. => Ganzen Artikel lesen …
Mathematik
Wenn x·y immer gleich 20 sein soll, also x·y=20 gelten soll dann sind x und y zueinander antiproportional. x=2 und y=10 würde hier zum Beispiel die Gleichung lösen. Wenn man nun x doppelt so groß macht, wie es vorher war, und dabei gleichzeitig y halb so groß, dann geht die Gleichung immer noch auf: x=4 und y=5 geben malgerechnet auch 20. Statt antriproportional sagt man auch umgekehrt proportional. Siehe mehr zu diesem Thema im Artikel => umgekehrt proportionale Zuordnung
Mathematik
Die Funktion f(x)=4x ist gleichzeitig auch eine eindeutige Zuordnung: sie ordnet jeder Zahl, die man für x einsetzen kann, eindeutig genau eine Zahl zu. Eindeutig meint hier, dass nicht zum Beispiel gar keine, zwei oder mehr Zahlen zugeordnet werden. Ein anderer Namen für eine eindeutige Zuordnung ist auch => Funktion
… siehe unter => Funktionsvorschrift
… als mathematischer Fachbegriff auch => Bijektion
Mathematik
Ist f(x) = x² eine Funktion, eine Zuordnung oder beides? Was Funktionen und Zuordnungen miteinander zu tun haben ist hier kurz erklärt. => Ganzen Artikel lesen …
Funktion
Zum Beispiel: y=4x+1: jede lineare Zuordnung im Sinne der Schulmathematik ist eine => Lineare Funktion
… in der Fachsprache der Mathematik dasselbe wie eine => Injektion
Mengenlehre
Man kann jedem Haus in einer Straße die Bewohner dieses Hauses zuordnen. Wenn in einem Haus mehr als nur eine Person wohnt, dann kann man jedem Haus mehrere Personen zuordneten. Eine solche Zuordnung ist nicht mehr eindeutig sondern => mehrdeutig
… Beispiele unter => keine Funktionen
… Beispiele unter => keine Funktionen
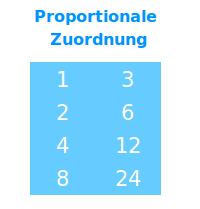Proportionale Zuordnung
Übersicht
Hier wird kurz eine Definition vorgestellt und wie man proportionale Zuordnungen erkennt. => Ganzen Artikel lesen …
… z. B. y=x²+4, meint dasselbe wi eine => quadratische Funktion
… als mathematisches Fachwort auch => Surjektion
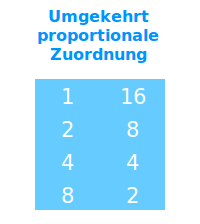Umgekehrt proportionale Zuordnung
… das Thema steht unter => umgekehrt proportionale Funktion
… meint dasselbe wie => Umgekehrt proportionale Funktionen
… Beispiele unter => keine Funktionen
… Beispiele unter => keine Funktionen
… siehe unter => Funktion oder Zuordnung [Vergleich]
Mathematik
Ist f(x) = x² eine Funktion, eine Zuordnung oder beides? Was Funktionen und Zuordnungen miteinander zu tun haben ist hier kurz erklärt. => Ganzen Artikel lesen …
Bedeutung
Die Worte Zunahme und Relation werden in der Mathematik oft gleichbedeutend, also als Synonyme verwendet. Dazu stehen hier kurz aufgelistet einige Fragen. => Ganzen Artikel lesen …
… Beispiele unter => keine Funktionen
… Beispiele unter => keine Funktionen
x ↦ y
Eine Zuordnung ist eine Regel, nach der man Elementen einer Menge Elemente einer anderen Menge zuweist. Es gibt verschiedene Arten; zur Kennzeichnung verwendet man verschiedene => Zuordnungspfeile
Übersicht
Eine Zuordnung ist eine Regel, nach der man Elementen einer Menge Elemente einer anderen Menge zuweist. Es gibt verschiedene Arten, für die es verschieden Arten von Pfeilen gibt. Diese werden hier kurz vorgestellt. => Ganzen Artikel lesen …
… Beispiele unter => keine Funktionen
