gibt immer Zahl·x
f(x) = 4 aufgeleitet gibt F(x) = 4x. Allgemein gilt: man muss hinter die Zahl nur ein x schreiben und hat dann eine Stammfunktion. Dazu stehen hier noch einige Beispiele. => Ganzen Artikel lesen …
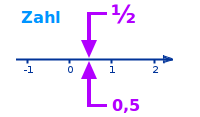 Zahl
Zahl
Mathematik
Eine Zahl ist ein Begriff, das heißt eine Vorstellung, von einem Wie-Viel oder Wie-Vielen. Die Zahl selbst ist etwas anderes als ihre Darstellung. Jeder eigene Punkt auf der Zahlengerden ist eine eigene Zahl. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
F(x) bestimmen
Definition: Als Aufleiten bezeichnet man die Bestimmung einer Stammfunktion F(x) zu einer gegebenen Funktion f(x). Das Aufleiten ist die Gegenoperation des Ableitens: f(x) aufgeleitet gibt F(x). Und F(x) abgeleitet gibt f(x). Hier werden kurz Verfahren dazu vorgestellt. => Ganzen Artikel lesen …
Ergibt immer 0
f(x)=5 ergibt abgeleitet f'(x)=0: besteht der Funktionsterm nur aus einer Zahl, oder kann er ganz in eine Zahl umgeformt werden, dann ist die Ableitungsfunktion immer f'(x)=0. Das wird hier erklärt und hergeleitet. => Ganzen Artikel lesen …
… ist immer Zahl mal x, mehr unter => Zahl aufgeleitet
… gibt 0, mehr unter => Nullfunktion aufleiten
… gibt immer Zahl mal x, mehr unter => Zahl aufleiten

