Wurzel aus negativer Zahl
z. B. √-4
Eine Wurzel ist per Definition immer nur eine positive Zahl oder die Zahl 0. Die Wurzel von der Zahl 4 ist nur die Zahl 2. Obwohl die -2 mit sich selbst malgenommen auch 4 ergäbe, bezeichnet man sie nicht als Wurzel. Aus der Zahl -4 gibt es gar keine reelle Zahl, die mit sich selbst multipliziert wieder -4 gäbe. Negative Zahlen haben niemals eine reelle Wurzel. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Wurzel
Definition
Die Wurzel von der Zahl 16 ist die 4. Denn: 4 mal 4 gibt wieder 16. Man schreibt kurz: √16=4. Die Wurzel von irgendeiner Zahl z ist diejenige nicht negative Zahl, die mit sich selbst malgenommen wieder die Zahl ergibt. Diese Definition gilt für die umgangssprachlich gesprochen „normale“ Wurzel, die man auch Quadratwurzel nennt. => Ganzen Artikel lesen …
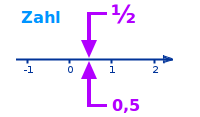
Zahl
Mathematik
Eine Zahl ist ein Begriff, das heißt eine Vorstellung, von einem Wie-Viel oder Wie-Vielen. Die Zahl selbst ist etwas anderes als ihre Darstellung. Jeder eigene Punkt auf der Zahlengerden ist eine eigene Zahl. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… wo es sie doch gibt steht unter => Wurzel aus negativer Zahl
… wo es sie doch gibt steht unter => Wurzel aus negativer Zahl
… gibt es nicht, mehr unter => Wurzel aus negativer Zahl
… wo es sie doch gibt steht unter => Wurzel aus negativer Zahl
… es gibt keine Lösung, mehr unter => Diskriminante bei pq-Formel
… wo es sie doch gibt steht unter => Wurzel aus negativer Zahl
