Definition
9/25 ⭢ „gewurzelt“ ⭢ 3/5: die Wurzel aus einem Bruch ist der Bruch, der mit sich selbst malgenommen wieder den ursprünglichen Bruch gibt. Probe: 3/5 mal 3/5 gibt wieder 9/25. Eine Anleitung steht unter => Wurzel aus Bruch ziehen
 Wurzel
Wurzel
Definition
Die Wurzel von der Zahl 16 ist die 4. Denn: 4 mal 4 gibt wieder 16. Man schreibt kurz: √16=4. Die Wurzel von irgendeiner Zahl z ist diejenige nicht negative Zahl, die mit sich selbst malgenommen wieder die Zahl ergibt. Diese Definition gilt für die umgangssprachlich gesprochen „normale“ Wurzel, die man auch Quadratwurzel nennt. => Ganzen Artikel lesen …
 Bruch
Bruch
z. B. ½
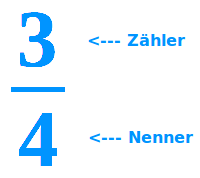
Als Bruch bezeichnet man jede Zahl, die mit einem Bruchstrich in der Form ⅖ oder 3/4 geschrieben ist. Die Zahl links oder oben vom Bruchstrich ist der Zähler, die Zahl rechts oder unten vom Bruchstrich der Nenner. Im engeren Sinn dürfen der Zähler und der Nenner jeweils nur eine ganze Zahl sein dürfen (z. B. -4, 5 oder 111). In einem verallgemeinerten Sinn dürfen Zähler und Nenner jede beliebige Reelle Zahl sein. Lediglich der Nenner (unten) in keinem Fall den Wert Null annehmen. [1] Mehr dazu unter => Bruchzahl
… siehe unter => Wurzel aus Bruch
… 4/9 wird zu 2/3 => Wurzel aus Bruch ziehen
… siehe unter => Wurzel aus Bruch
… Wurzel aus 9/16 gibt 3/4, mehr unter => Wurzel aus Bruch ziehen
Beispiele
4/9 gibt „gewurzelt“ 2/3: hier stehen einige Beispiele mit Zahlen zu Brüchen aus denen die Wurzel gezogen wurde. Wurzel meint hier die übliche Quadratwurzel. => Ganzen Artikel lesen …
… Wurzel aus 9/16 gibt 3/4, Erklärung unter => Brüche radizieren
Methoden
√(25/100) ist dasselbe wie √25/√100 und gibt weiter vereinfacht 5/10: um aus einem Bruch die Wurzel zu ziehen, kann man einzeln die Wurzel aus dem Zähler (oben) und danach aus dem Nenner (unten) ziehen. Daneben gibt es noch eine zweite Möglichkeit. Beide Methoden sind hier kurz mit einem Zahlenbeispiel vorgestellt. => Ganzen Artikel lesen …

