 Wellenpaket
Wellenpaket
Physik
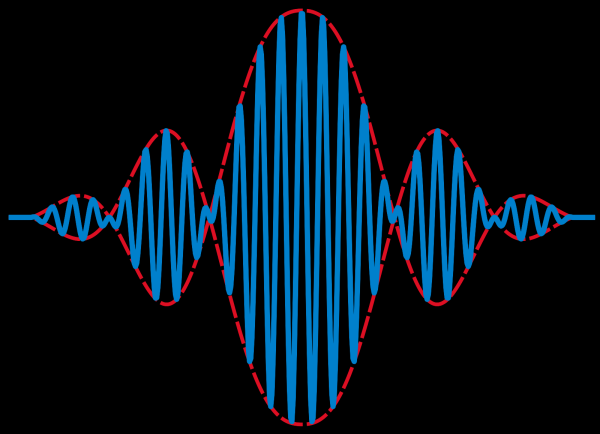
Ein Wellenpaket [5], eine Wellengruppe oder ein Wellenzug entsteht aus der Überlagerung mehrerer Wellen. Sind die einzelnen Wellen bezüglich ihrer Wellenlänge passend gewählt, können sie sich fast überall im Raum nahezu vollständig auslöschen. Nur in einem engen Raumbereich kommt es zu erhöhten Amplituden, die dann als Paket durch den Raum zu wandern scheinen [6]. Ein Wellenpaket hat keine einzelne Wellenlänge sondern eine Verteilung von Wellenlängen. Den eng lokalsierten Bereich eines Photons beispielweise kann man als Wellenpaket modellieren. Dass solche Wellen nicht infolge von Dispersion [7] auseinanderlaufen müssen zeigt das Beispiel des Solitons [8]. Zur mathematischen Modellierung dient unter anderem auch das sogenannte Wavelet [9]. Siehe auch => Materiewelle
… als Sedimentstruktur siehe unter => Rippel
Physik
Eine Welle im physikalischen Sinn ist eine Schwingung, die sich im Raum ausbreitet. Als Wellenphase kann man dabei den momentanen Zustand eines Oszillators, zum Beispiel eines Wasserteilchen, auffassen. Ein solcher Zustand kann zum Beispiel: das Teilchen ist auf der Hälfte einer ganzen Schwingung. Gibt man das als Anteil von 360° an, spricht man auch von einem Phasenwinkel. Die Wellenphase ist ausführlich erklärt im Artikel zur => Phasengeschwindigkeit
Drei mal drei Steine in einem Quadrat
Das Wort Neunerpaket stammt aus der Welt der Kieler Zahlenbilder. Man meint damit die folgende Figur aus Steine, Erbesen oder sonstigen Dingen: => Ganzen Artikel lesen …
Selbstbau
Eine Wellenwanne [1] (Englisch: ripple tank) ist eine flache meist rechteckige Wanne mit durchsichtigem Boden. In der Physik wird sie benutzt, um typische Phänomene rund um Wasserwellen anschaulich zu machen. Hier stehen Tipps und Erfahrungen rund um den Bau einer möglichst einfachen Wellenwanne mit Baumarktartikeln und für kleines Geld. => Ganzen Artikel lesen …

