 Würfelvolumen
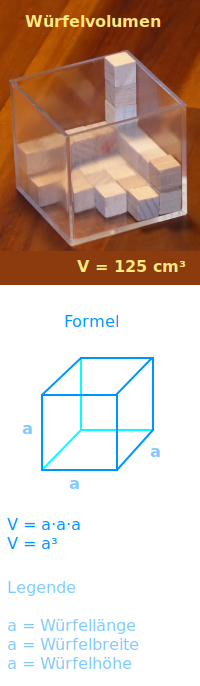
Würfelvolumen
Geometrie
Wie viel Raum ein Würfel braucht: V = Länge mal Breite mal Höhe. Da bei einem Würfel die Länge, Breite und Höhe aber immer gleich lang sind, kann man auch kurz sagen: Länge mal Länge mal Länge. Man kann das Volumen angeben in z. B. cm³ (Kubikzentimeter), Milliliter oder Litern. => Ganzen Artikel lesen …
Beispiele
Ein Würfel, der 2 Zentimer lang, breit und hoch ist hat ein Volumen von 8 Kubikzentimeter: die Länge der Würfelkanten (sind alle gleich) hoch drei gerechnet gibt das Volumen des Würfels. Hier steht eine Liste mit den Ergebnissen von einigen Beispielrechnungen. => Ganzen Artikel lesen …
 Kegelvolumen
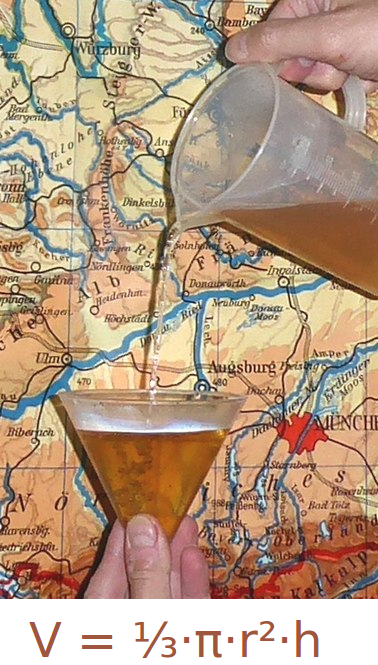
Kegelvolumen
V = ⅓·π·r²·h
Ein Kegel ist ein spitzer Körper mit kreisförmiger Grundfläche. Sein Volumen V kann zum Beispiel angegeben werden in Kubikmetern (m³), Kubikzentimern (cm³) oder Litern. Hier werden der Sinn und die Berechnung kurz erklärt. => Ganzen Artikel lesen …
Geometrie
Das Volumen gibt an, wie viel Raum (3D) ein Körper einnimmt oder wie viel Flüssigkeit man in einen Hohrlaum hineinfüllen kann. Man gibt Volumen zum Beispiel an in cm³, m³ oder auch Litern. Siehe unter => Volumenformeln
… meint eigentlich dasselbe wie ein => Quadrat
Volumen, Oberfläche, Masse, Diagonale
Ein Würfel hat sechs Quadrate als Seitenflächen. Und er hat 12 gleich lange Kanten. Aus diesen Angaben lassen sich weitere Eigenschaften berechnen. Hier stehen kurz einige Beispiele. => Ganzen Artikel lesen …
Formeln
Würfelvolumen gleich: Länge mal Breite mal Höhe. Beispiel: ein Würfel ist 2 cm lang, breit und hoch. Dann beträgt sein Volumen 2·2·2 Kubikzentimeter oder kurz: 8 cm³ => Ganzen Artikel lesen …

