Verknüpfung
Mathematik
Verbindung nach festen Regeln mit (neuem) Ergebnis: die Funktionen f(x)=2x und h(x)=x² kann man zum Beispiel über die Addition verknüpfen zu v(x)=2x+x². Das ist hier näher erklärt. => Ganzen Artikel lesen …
(Mathematische) Regeln, zur Zuordnung mathematischer Objekte wie Zahlen
- => Einstellige Verknüpfungen
Verdampfung
Definition
Die Verwandlung von einer Flüssigkeit in ein Gas nennt man Verdampfung. Man unterscheidet zwei Arten der Verdampfung: die Verdunstung und das Sieden. Das Kochen, etwa von Wasser, gehört dabei physikalisch zum => Sieden
Vergütung hat mehrere Bedeutungen:
Vergütung nennt man die Bezahlung in Geld für eine Dienstleistung. Man sagt zum Beispiel: Der Arzt bekam eine hohe Vergütung für seine Behandlung. Man würde aber nicht sagen: „Der Bäcker bekam eine Vergütung von 30 Cent für das Brötchen“ (Brötchen sind keine Dienstleistung) => Ganzen Artikel lesen …
… auch Verbindungs-, oder Klammergesetz sind andere Worte für das => Assoziativgesetz
… [Rechen]Regel die nur genau eine Eingabe braucht, mehr unter => einstellige Verknüpfung
… eine Verknüpfung mit genau zwei Operanden => zweistellige Verknüpfung
Drei Eingaben
Eine dreistellige Operation nennt man auch dreistellige Verknüpfung: wenn man drei Vektoren hat, dann kann man ihnen gemeinsam ein Spatprodukt zuordnen. Eine Rechnung, die drei Eingaben benötigt um sie ausführen zu können nennt man dreistellig. Siehe mehr zum Beispiel unter => Spatprodukt
Definition
Eine (Rechen)Regel, die nur eine Zahl als Eingabe braucht: eine einstellige Verknüpfung (auch unäre oder monadische Verknüpfung) ist in der Mathematik eine Verknüpfung mit nur einem Operanden. Ein einfaches Beispiel einer einstelligen Verknüpfung ist das unäre Minus zur Bildung der Gegenzahl einer Zahl. => Ganzen Artikel lesen …
Beispiele für (Rechen)Regeln, die nur eine Zahl als Eingabe brauchen
Quadrieren: Macht zum Beispiel aus 4 die 16. => Ganzen Artikel lesen …
… [Rechen]Regel, die nur genau eine Eingabe braucht, mehr unter => einstellige Verknüpfung
Mehrdeutigkeit durch unklare Hierarchie
Das Wort Verknüpfung wird in der Mathematik einmal als Überbegriff und einmal als darunterfallenden Sonderfall verwendet. Das führt zu schwer erschließbaren Texten in Lehrwerken. => Ganzen Artikel lesen …
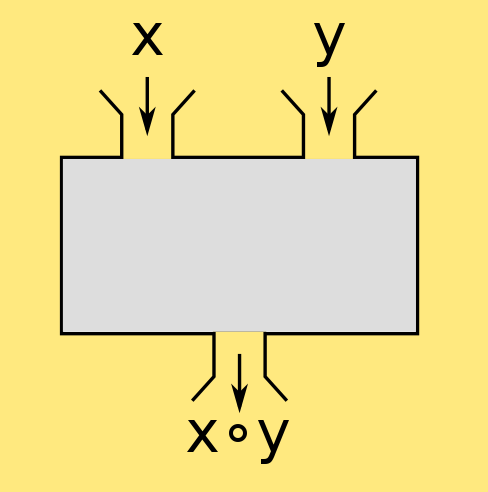
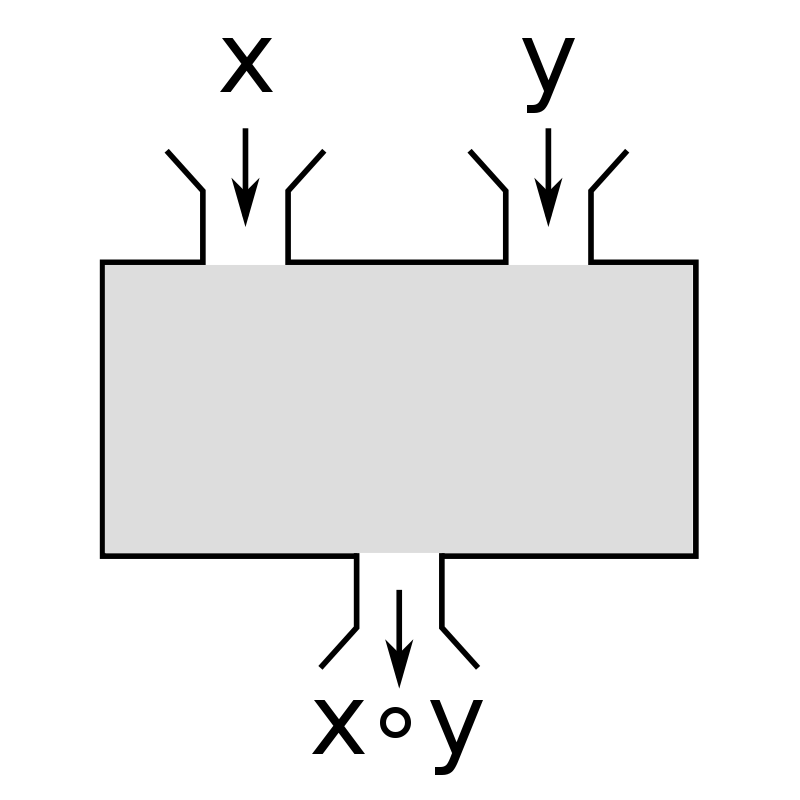Zweistellige Verknüpfung
Braucht zwei Eingaben
Eine zweistellige Verknüpfung, auch binäre Verknüpfung genannt, ist in der Mathematik eine Verknüpfung, die genau zwei Operanden besitzt. Zweistellige Verknüpfungen treten insbesondere in der Algebra sehr häufig auf und man spricht dort abkürzend auch von Verknüpfung ohne den Zusatz zweistellig. => Ganzen Artikel lesen …
Beispiele für Verknüpfung die genau zwei Eingaben brauchen
-> P => Ganzen Artikel lesen …
Beispiele
4+3 oder 2·5: zweistellig nennt man Verknüpfung die genau zwei Eingaben brauchen. Hier stehen einige Beispiele dazu. => Ganzen Artikel lesen …
