Vektor normieren
Anleitung
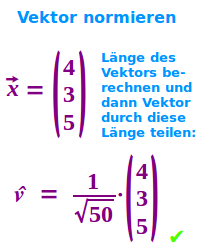
Einen Vektor zu normieren heißt, dass man seine Länge zu 1 macht. Die Richtung, in die der Vektor zeigt, wird dabei nicht verändert. Rechnerisch teilt man alle Koordinaten durch die Vektorlänge (Betrag): das Ergebnis ist ein Vektor mit derselben Richtung wie der Ausgangsvektor und mit der Länge 1. Hier steht das Verfahren Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
Vektor
↗ Definition
Als Vektor bezeichnet man in der Mathematik oft einen Pfeil in einem 2D- oder 3D-Koordinatensystem. Er wird oft mit zwei, drei oder auch mehr Zahlen - den Vektorkoordinaten - geschrieben. Diese Zahlen sagen nichts darüber aus, wo ein Vektor in einem Koordinatensystem liegt. Die Zahlen sagen nur, wie lang der Vektor ist und in welche Richtung er zeigt. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… also auf die Länge 1 bringen, siehe unter => Vektor normieren
Beispiel
Siehe auch => Ganzen Artikel lesen …
… macht man mit Hilfe einer sogenannten => Drehmatrix
… wie a-b, siehe unter => Vektordifferenz
