Torf
Definition
Torf bildet sich, wenn totes Pflanzematerial in Wasser gerät und dort nicht verrotet. Torf kann als Brennstoff und Dünger verwendet werden. Das ist hier kurz erläutert. => Ganzen Artikel lesen …
Übersicht
Das Tor als Ziel beim Fußball oder auch Tor als ein dümmlicher Typ. Für die Maße eines Tors im Fußball, siehe unter => Tor (Fußball)
Geometrie
Ein Rettungsring, eine ringförmige Weltraumkolonie oder ein Donut: Tori ist eine korrekte Mehrzahl von Torus. Ein Torus in der Geometrie ist ein ringartiger Körper. Hier stehen einige Beispiele. => Ganzen Artikel lesen …
Chemie
Bor - chemisches Zeichen B, Ordnungszahl 5 - ist ein in einer tetragonalen und zwei rhombischen Modifikationen vorkommendes, in kistalliner Form grauschwarzes, sehr hartes und reaktionsträges, nichtmetallisches chemisches Element. Siehe auch => Bor Datenblatt
… in der Elektrotechnik, kurz für einen => Transformator
MJ/kg
Trockener Torf hat mit rund 23 Millionen Joule für jedes Kilogramm, kurz 23 MJ/kg, einen recht hohen Brennwert, gut zweieinhalbmal so viel wie Rohbraunkohle. MJ heißt Megajoule und meint so viel wie Millionen Joule. Wärme und Strom aus Torf gilt als fossile Energie. Torf wurde früher in großem Umfang als Brennstoff abgebaut, bis zum Jahr 2020 sogar zur Stromerzeugung (West Offaly Power Station, Ireland). Das gilt inzwischen aus mehreren Gründen als umweltschädlich. Lies mehr zu dem Thema im Artikel zu => Torf
Physik
Die Divergenz eines Vektorfeldes gibt für jeden Punkt des Feldes an, wie stark in seiner Umgebung die Vektoren auseinander streben. Die Divergenz selbst ist eine reine Zahl, also ein Skalar. Die Divergenz spielt unter anderem bei Strömungsfeldern und bei den Maxwell-Gleichungen der Elektrodynamik eine Rolle. => Ganzen Artikel lesen …
… flog in 12 Sekunden 37 Meter, mehr unter => Wright Flyer I
… Rechenbeispiel unter => Allgemeine Form in Faktorisierte Form
… Rechenbeispiel unter => Faktorisierte Form in Normalform
… Rechenbeispiel unter => Faktorisierte Form in Scheitelpunktform
… es gibt mehrere, siehe unter => Kondensatorformeln
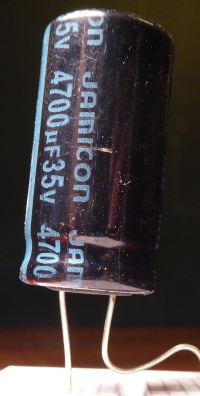Kondensatorformeln
Elektrotechnik
Kapazität, Energie, Auf- und Entladestrom und spannung: hier stehen die wichtigsten Formeln zu einem elektrischen Kondensator in der Übersicht. => Ganzen Artikel lesen …
Kreissektorfläche
… ist dasselbe wie die => Kreisausschnittsfläche
… etwa in cm², siehe unter => Kreisausschnittsfläche berechnen
… zum Beispiel in cm², siehe unter => Kreissektorfläche
… Rechenbeispiel unter => Faktorisierte Form in Normalform
… z. B. von (x+3)(x+2) => Nullstellen aus faktorisierter Form
Physik
Ein Vektorfeld gilt in einem Bereich als quellfrei oder quellenfrei, wenn seine Feldlinien nirgends einen Anfang haben. Mathematisch ist das gleichbedeutend mit der Aussage, dass die Divergenz dort nirgend größer ist als 0. Es ist zudem frei von Senken, wenn die Divergenz nirgends kleiner ist als 0. Oft heißt quellenfrei aber etwas unpräzise, dass die Divergenz 0 sein soll. Eindeutiger ist es hier von einem divergenzfreien Feld zu sprechen. Siehe auch => Divergenz eines Vektorfeldes
… in der Physik und Vektoranalysis auch => quellenfreies Vektorfeld
Rotation eines Vektorfeldes
Physik
Die Rotation eines Vektorfeldes hängt anschaulich eng mit Wirbeln [1], Winkelgeschwindigkeiten [2] und der Rotation von Probekörpern um sich selbst in einem Strömungsfeld [3] von Flüssigkeiten [4] zusammen. Das ist hier mit Rechenbeispielen erklärt. => Ganzen Artikel lesen …
… etwas Hub- oder Tragschrauber heißen auch => Drehflügler
… Rechenbeispiel unter => Faktorisierte Form in Scheitelpunktform
… Rechenbeispiel unter => Scheitelpunktform in faktorisierte Form
… etwa 23 MJ/kg => Brennwert Torf
Torfmoos
Biologie
Torfmoos (Sphagnum) steht für eine Gattung - also mehrere Arten - von Moosen. Torfmoose bilden oft das Ausgangsmaterial für die Bildung von Torfen in Hoch- und Niedermooren. Die Pflanzen sind hier kurz vorgestellt. => Ganzen Artikel lesen …
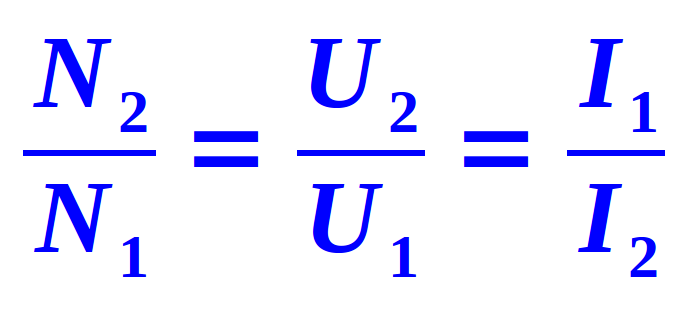Transformatorformel
Elektrotechnik
Ein Transformator ändert die Spannung (Voltzahl) bei Wechselstrom. Gleichzeitig wird dabei immer auch die elektrische Stromstärke (Amperezahl) mitverändert. Hier steht die Formel mit Legende. => Ganzen Artikel lesen …
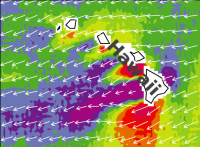Vektorfeld
Mathematik
Angenommen auf einer Wetterkarte ist für jeden Punkt auf der Erdoberfläche die Windrichtung mit einem Pfeil eingetragen. Die Länge des Pfeiles steht dabei für die Stärke des Windes. Diese Darstellung wäre ein Vektorfeld: für jeden Punkt eines Raumes (auch einer Ebene) ist ein Vektor zugeordnet. => Ganzen Artikel lesen …
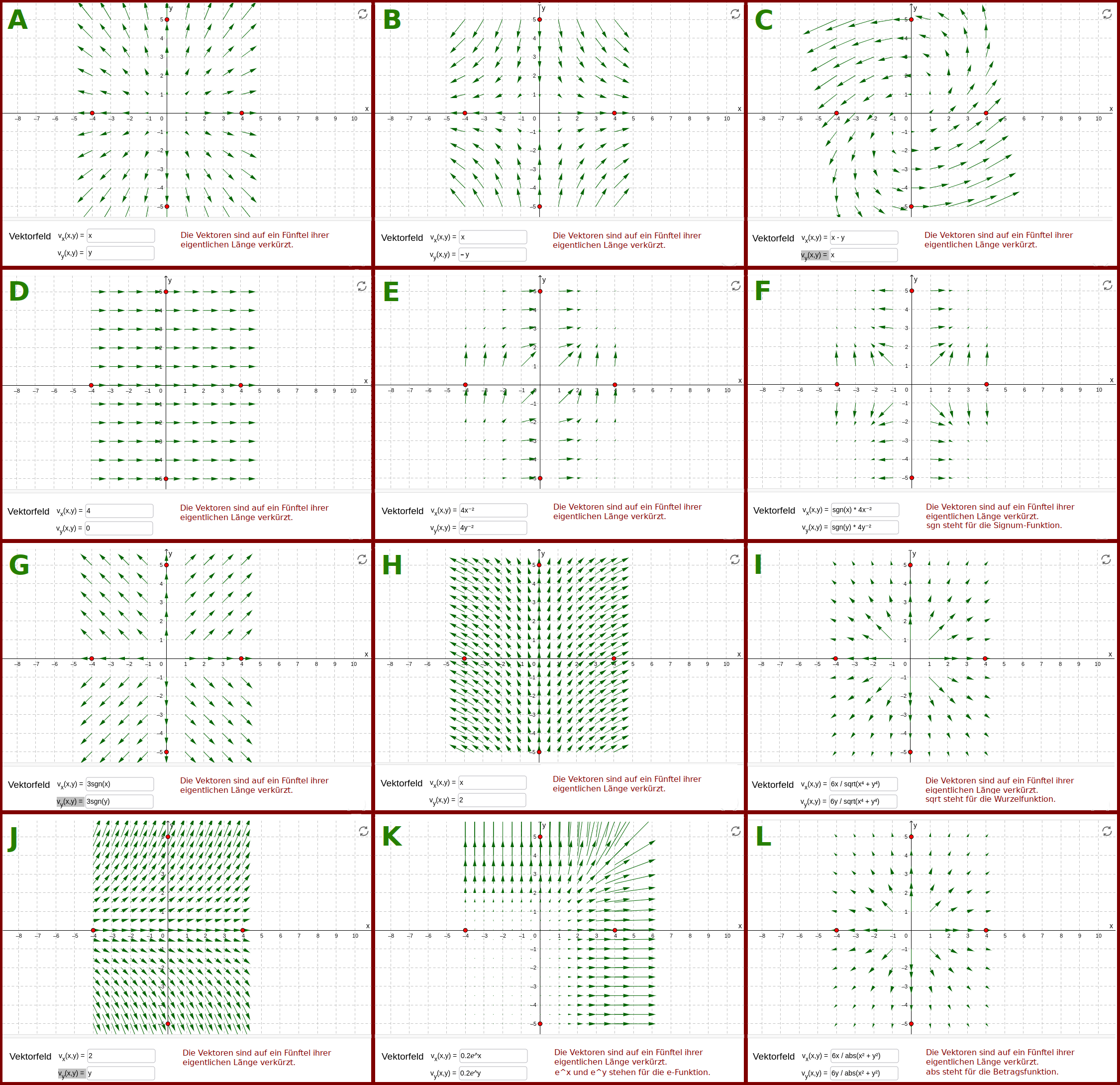Vektorfelder
Beispiele
Wie stark und in welche Richtung der Wind an verschiedenen Orten weht, kann man gut mit Pfeilen auf einer Landkarte darstellen. Solche Windfelder sind ein typisches Beispiel für sogenannte Vektorfelder. Die Vektoren sind dabei die Pfeile. Hier stehen einige weitere Beispiele dazu. => Ganzen Artikel lesen …
… siehe unter => Vektoranalysis
Vektorfuss
Ohne Spitze
Wird ein Vektor als Pfeil veranschaulicht, dann kann man das Ende des Vektors ohne die Pfeilspitze den Vektorfuß nennen. Auf ihn würde man den Pfeil stellen, wenn man ihn wie einen Speer in die Erde steckt. Das lange gerade Stück des Vektors ist dann der => Vektorschaft [auch Vektorachse]
Physik
Als Zirkulation eines Vektorfeldes bezeichnet man das Integral entlang einer geschlossenen Linie, bei dem die Vektorkomponenten in tangentialer Richtung dieser Linie integriert, also gedanklich aufaddiert werden [1]. Siehe auch => Vektoranalysis
