Übersicht
Die Subtraktion ist in der Mathematik die Erweiterung der Idee des Abziehens (Minusrechnen). Während sich das Minusrechnen in der Grundschule meist auf Abzieh- und eventuell auch Ergänzungsaufgaben mit positiven Ergebnissen [1] beschränkt, werden unter Subtraktion auch Rechnungen mit negativen Zahlen, Vektoren oder Matrizen behandelt [2]. => Ganzen Artikel lesen …
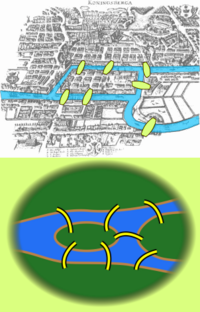Abstraktion
Denkschritt
Das lateinische Wort Abstrahieren heißt wörtlich übersetzt so viel wie abziehen [1]. Die Abstraktion bezeichnet einen Denkprozess, der von einer Fülle von Merkmalen der Vorstellungsganzen eines oder mehrere Betandteile abgesondert werden [1], und zwar solche die man für nicht wesentlich [1] oder bloß individuell (subjektiv) [3] hält. Die Abstraktion führt oft zur Bildung übergeordneter Begriffe [2]. Man kann aus der Fülle der verschiedenen Erscheinungen des Wetters auf Begriffe wie Wirbelsturm oder Nebel kommen. Dazu stehen hier kurz Beispiele. => Ganzen Artikel lesen …
Ein Fremdwort für Schrumpfung, Zusammenziehen
Kontraktion - wörtlich: zusammenziehen - steht oft für Schrumpfungsvorgänge. Der Begriff kommt unter anderem in der Astronomie, der Relativitätstheorie und der Materialkunde vor. => Ganzen Artikel lesen …
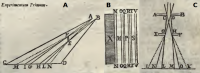Diffraktion
Physik
Diffraktion, auch Inflexion [3] heißt in der Physik dasselbe wie Beugung [2]. Damit ist insbesondere die Ausbreitung von Licht in Bereiche gemeint, in die es bei ausschließlich geradliniger Bewegung im Sinne einer Strahlenoptik nicht gelangen dürfte; und zwar verursacht durch undurchsichtige Körper in dessen direkter Nähe das Licht vorbei geht [4]. Der Begriff wurde von Francesco Maria Grimaldi (1618 bis 1663) geprägt [2] und von Isaac Newton gemieden und durch das Wort Inflexion ersetzt [5]. Diffraktion als Folge von Wellenphänomenen geht immer auch mit Effekten der Interferenz einher [6]. Siehe mehr unter => Beugung
… man 3/4 minus 5/8 rechnet steht unter => Brüche subtrahieren
… es gibt keine besondere Regel, mehr unter => Wurzel minus Wurzel
… z. B. 2¾ - 1½ => Gemischte Zahl minus gemischte Zahl
… z. B. 2¾ - 1½ => Gemischte Zahl minus gemischte Zahl
… z. B. 2¾ - 1½ => Gemischte Zahl minus gemischte Zahl
Zahl selbst
Das inverse Element einer Verknüpfung von zwei mathematischen Objekten muss als Ergebnis immer das sogenannte neutrale Element dieser Verknüpfungsart gegeben. Das neutrale Element der Subtraktion ist die Zahl 0. Entsprechend kann eine Zahl in einer Subtraktion nur mit sich selbst verknüpft werden, soll am Ende 0 herauskommen. Als Konsequenz daraus ist das inverse Element der Subtraktion die Zahl selbst. Siehe auch => inverse Elemente
… siehe unter => Minuskette
… wie etwa 10-(x+5) oder (3x+8)-(2x+Siehe unter => Minusklammern auflösen
… wie etwa 10-(x+5) oder (3x+8)-(2x+Siehe unter => Minusklammern auflösen
… siehe unter => Matrizen subtrahieren
… z. B. , mehr unter => Minuszahl minus Minuszahl
… 4-(-1) ist wie 4+1, Erklärung unter => Negative Zahl subtrahieren
… ist wie plus, mehr unter => Minuszahl minus Minuszahl
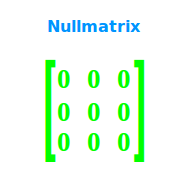Neutrales Element der Matrizensubtraktion
Nullmatrix
Die Nullmatrix: sie kann von einer anderen Matrix abgezogen, also subtrahiert werden und verändert dabei an der Ausgangsmatrix nichts. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
… ist die Null, mehr unter => neutrales Element
… wie 5³-5² = 100, siehe unter => Potenz minus Potenz
… wie 5³-Siehe unter => Potenz minus Potenz
… so etwas wie 2³-2² => Potenzen mit gleicher Basis subtrahieren
… 378 - 96 => schriftlich subtrahieren
Wie man Minus als Plus rechnet
In der Grundschule war das Minusrechnen eine eigene Rechenart. Dort rechnete man nur mit den sogenannten natürliche Zahlen wie 1; 2; 3; 4 und so weiter. Später kamen dann die negativen Zahlen dazu. Mit Hilfe der negativen Zahlen lässt sich die Subtraktion (Minusrechnen) jetzt als ein Sonderfall der Addition handhaben: 8 minus 3 ist dann dasselbe wie 8 + (-3). Allgemein gilt: die Subtraktion einer Zahl ergibt das Gleiche wie die Addition ihrer Gegenzahl. Siehe auch => Gegenzahl
… ist wie dazurechnen, mehr unter => Negative Zahlen subtrahieren
Eine der vier Grundrechenarten, das Minusrechnen
Minuend - Subtrahend = Differenz => Ganzen Artikel lesen …
… z. B. 2¾ - 1½ => Gemischte Zahl minus gemischte Zahl
… wie etwa 10-(x+5) oder (3x+8)-(2x+Siehe unter => Minusklammern auflösen
… wie etwa 10-(x+5) oder (3x+8)-(2x+Siehe unter => Minusklammern auflösen
… 4-(-1) ist wie 4+1, Erklärung unter => Negative Zahl subtrahieren
… mehrere Fälle sind beschrieben unter => Subtrahieren mit negativen Zahlen
… mehrere Fälle sind beschrieben unter => Subtrahieren mit negativen Zahlen
… wie etwa 10-(x+5) oder (3x+8)-(2x+Siehe unter => Minusklammern auflösen
… z. B. , mehr unter => Minuszahl minus Minuszahl
… z. B. , mehr unter => Minuszahl minus Minuszahl
