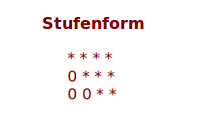
Stufenform

Gauß-Algorithmus

Die Stufen- oder Treppenform ist innerhalb des Gauß-Algorithmus, ein Zwischenergebnis: unten links in der Ecke einer Matrix stehen Nullen in einer bestimmten Anordnung. Das ist hier näher erklärt. => Ganzen Artikel lesen …

Summenform

3x+x ist eine Summenform

Was als Summe geschrieben ist nennt man kurz eine Summenform. Ein Beispiel ist 3x+x. Die Bestandteile 3x und x sind dabei die Summanden. Den ganzen Term 3x+x nennt man eine Summe. Vor allem bei Funktionen spricht man von einer Summenform. Hier stehen einige Beispiele und häufige Rechenarten dazu. => Ganzen Artikel lesen …

4: Stufenbau

… in der Evolutionstheorie, siehe unter => Stufenbau der Materie

6: Treppenstufenform

… beim Gauß-Algorithmus dasselbe wie die => Stufenform

7: LGS mit Stufenform lösen

… mit der Stufenform und den Nullen unten links, siehe unter => Gauß-Algorithmus

8: Lineares Gleichungssystem über Stufenform lösen

… mit der Stufenform und den Nullen unten links, siehe unter => Gauß-Algorithmus

9: Methode mit Stufenform

… mit der Stufenform und den Nullen unten links, siehe unter => Gauß-Algorithmus

10: Methode mit Zeilenstufenform

… mit der Stufenform und den Nullen unten links, siehe unter => Gauß-Algorithmus

12: Stufenform-Algorithmus

… mit der Stufenform und den Nullen unten links, siehe unter => Gauß-Algorithmus

13: Stufenform-Methode

… mit der Stufenform und den Nullen unten links, siehe unter => Gauß-Algorithmus

14: Stufenform-Verfahren

… mit der Stufenform und den Nullen unten links, siehe unter => Gauß-Algorithmus

15: Verfahren mit der Stufenform

… zum Lösen von linearen Gleichungssystemen => Gauß-Algorithmus