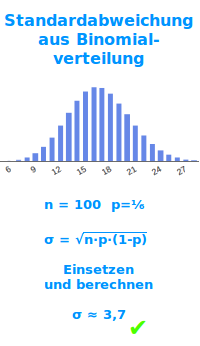
Standardabweichung aus Binomialverteilung
σ = √(n·p·(1-p))
Die Standardabweichung gibt in etwa an, wie weit die Trefferhäufigkeiten im Schnitt von ihrem gemeinsamen Durchschnittswert entfernt sind. Sie spielt auch eine Rolle im Zusammenhang mit dem Satz von Moivre-Laplace. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
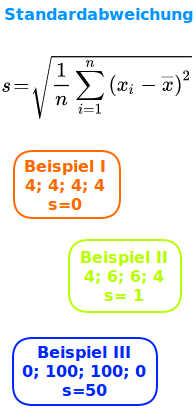Standardabweichung
σ: Ein Streuungsmaß aus der Statistik
Die Standardabweichung Sigma gibt an, wie weit die Zahlen einer Zahlenliste von ihrem gemeinsamen Mittelwert entfernt sind. Die Zahlenliste 3;3;3;3 hat eine Standardabweichung von 0. Die Zahlenliste 1;1;5;5 hat eine Standardabweichung von 2. Hier wird kurz erklärt, was die Standardabweichung als Streuungsmaß bedeut und wie man sie berechnet. => Ganzen Artikel lesen …
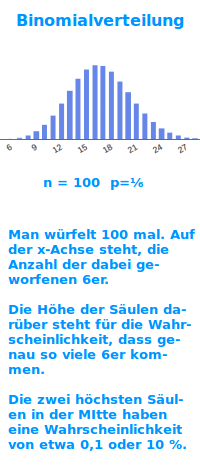Binomialverteilung
B(n,k,p)
Als Binomialverteilung bezeichnet man eine übersichtsartige Darstellung der Wahrscheinlichkeiten aller möglichen Ergebnisse einer Bernoulli-Kette: Die Verteilung gibt an, wie sich die 100 % dass irgendetwas passiert auf die einzelnen Ergebnisse verteilen, daher das Wort Verteilung. Eine Binomialverteilung kann eine Tabelle, ein Graph oder ein Histogramm sein. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… Berechnung unter => Standardabweichung aus Binomialverteilung
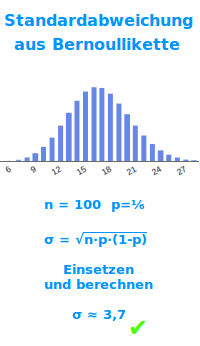Standardabweichung aus Bernoulli-Kette
σ = √(n·p·(1-p))
Einer Binomialverteilung liegt immer einer Bernoulli-Kette als Modell zugrunde. Die Formel oben gilt deshalb sowohl für Bernoulli-Ketten als auch Binomialverteilungen. Eine ausführliche Erklärung steht unter => Standardabweichung aus Binomialverteilung
Berechnung
Die Varianz und daraus die Wurzel gibt die Standardabweichung. Wenn die Varianz 4,0 ist, dann ist die Standardabweichung 2,0. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
Definition
Normalverteilung mit mü=0 und sigma=1: die mathematische Funktion zur Beschreibung normalverteilter Zufallswerte heißt Gauß-Funktion (die Glockenkurve). Setzt man in diese Formel den Erwartungswerte mü=0 und die Standarabweichung sigma=1 ein, dann erhält man die sogenannte Standardnormalverteilung. => Ganzen Artikel lesen …
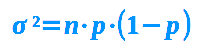Varianz aus Binomialverteilung
V = n·p·(1-p)
Die Varianz ist ein Streuungsmaß und sagt indirekt: wie weit liegen die einzelnen Werte, die in einer Verteilung auftreten, voneinander entfernt. Die Wurzel aus der Varianz ergibt die Standardabweichung. => Ganzen Artikel lesen …
… Wurzel aus (n·p·(1-p)), mehr unter => Standardabweichung aus Binomialverteilung
