f'(x) = cos(x)
Die elementare Sinusfunktion f(x) = sin(x) abgeleitet gibt f'(x) = cos(x). Enthält das Argument einen komplexeren Term, benutzt man noch die Kettenregeln: f(x) = sin(4x²-8x) gibt abgeleitet f'(x) = (8x-8)·sin(4x²-8x). Lies mehr dazu unter => Ableiten über Kettenregel
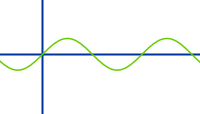Sinusfunktion
=> Ganzen Artikel lesen …
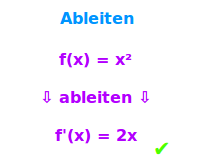Ableiten
Verfahren
Ableiten heißt f'(x) bilden: Ableiten im engeren Sinn heißt: Für einen Funktionsgraphen an einem Punkt die Steigung bestimmen. Im allgemeineren Sinn steht es dafür, die Ableitungsfunktion f'(x) zu bestimmen. Hier sind Regeln zur Bestimmung von f'(x) zusammengestellt. => Ganzen Artikel lesen …
f'(x) = cos(x)
Die elementare Cosinusfunktion f(x) = cos(x) abgeleitet gibt f'(x) = -sin(x). Enthält das Argument einen komplexeren Term, benutzt man noch die Kettenregeln: f(x) = cos(4x²-8x) gibt abgeleitet f'(x) = -(8x-8)·sin(4x²-8x). Lies mehr dazu unter => Ableiten über Kettenregel
Einsfunktion ableiten
f(x)=1 gibt abgeleitet f'(x)=0
Die Einsfunktion ist ein Sonderfall einer konstanten Funktion. Die Funktionsgleichung ist f(x)=1. Die Lösungsidee zur Ableitung ist es, die Funktion zu schreiben als f(x)=1·x⁰. Das x⁰ gibt als Wert immer 1. Man kann die Funktionsgleichung dann => ableiten über Potenzregel
Wie man die erste Ableitung bildet
Der Graph der Signum-Funktion besteht aus drei Abschnitten: für negative x-Werte ist er eine Gerade parallel zur x-Achse mit y=-1, für die Zahl ist es der Punkt (0|0) und für positive x-Werte ist er eine Gerade parallel zur x-Achse mit y=1. Der Graph verläuft also so gut wie überall als waagrechte Gerade mit der Steigung 0. Entsprechend muss auch die Ableitungsfunktion für alle x-Werte die Null ergeben. Die einzige Ausnahme ist x=0 selbst: hier macht der Graph einen Sprung (sogenannte Sprungstelle) und damit ist die Ableitung für x=0 nicht definiert. Der Graph ist dort => nicht differenzierbar
… ist cos (x), mehr unte => Sinusfunktion ableiten
