Geometrie
Jedes Dreieck hat immer genau drei Seitenhalbierende: Geraden die von einer Ecke des Dreiecks ausgehen und dann die gegenüberliegende Seite genau halbieren. Diese drei Seitenhalbierenden haben immer genau einen gemeinsamen Schittpunkt. Dieser Schnittspunkt ist dann auch immer der (mechanische) Schwerpunkt des Dreiecks. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Schnittpunkt
Definition
Ein Schnittpunkt ist ein gemeinsamer Punkt von zwei oder mehr Objekten. Ein Schnittpunkt muss also gleichzeitig zu mindestens zwei Objekten gehören. Objekte können sein: Mengen, Körper, Flächen, Linien, Geraden, Punktemengen etc. => Ganzen Artikel lesen …
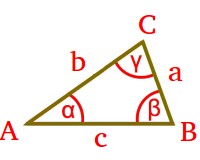Dreieck
ABC
Definition: Jede flache (2D) Figur mit genau drei Ecken und genau drei geraden Verbindungslinien zwischen den Linien ist ein Dreieck. Ein Dreieck ist damit eine Sonderfall eines Vielecks. Eine Themenübersicht steht auf der Seite => Dreiecksrechnung
Geometrie
Jedes Dreieck hat immer genau drei Winkelhalbierende, das sind Geraden, die durch eine Ecke des Dreiecks gehen und dann den Winkel zwischen den zwei aniegenden Dreiecksseiten halbieren. Diese drei Winkelhalbierenden haben immer genau einen gemeinsamen Schnittpunkt. Dieser Schnitt ist immer auch der Mittelpunkt des Inkreises des Dreiecks. Das ist hier näher erklärt. => Ganzen Artikel lesen …
gibt es für mehrere Figuren und Körper
- => Schnittpunkt der Seitenhalbierenden im Dreieck
Geometrie
In jedem Dreiechk schneiden sich die drei Höhenlinie immer in genau einem Punkt. Gibt es immer, hat aber keine besondere Bedeutung. Dieser Punkt hat aber keine besondere geometrische Bedeutung. Das ist hier kurz vorgestellt. => Ganzen Artikel lesen …
