… f(x)=a(x-d)²+e kurz auch nur SPF oder => Scheitelpunktform
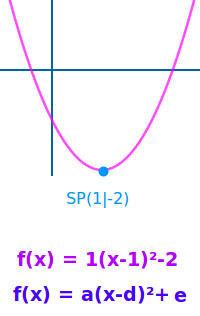Scheitelpunktform
f(x) = a·(x-d)² + e
Von quadratische Funktionen und Parabeln: aus der Scheitelpunktform y oder f(x) = a·(x²-d)²+e kann man leicht den Scheitelpunkt, die Öffnung und den y-Achsenabschnitt ablesen einer Parabel in einem xy-Koordinatensystem ablesen. Umgekehrt kann man sie leicht aufstellen, wenn man von einer Parabel den Scheitelpunkt SP und irgendeinen weiteren Punkt kennt. Das ist im Folgenden beschrieben. => Ganzen Artikel lesen …
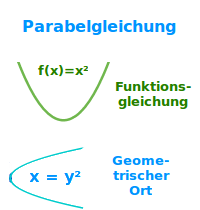Parabelgleichung
Definition
Der Graph einer quadratischen Funktion ist immer eine Parabel. Die Funktionsgleichung ist damit immer auch eine Parabelgleichung. Aber nicht jede Parabel in einem xy-Koordinatensystem kann als quadratische Funktion geschrieben werden. Das ist hier kurz erläutert. => Ganzen Artikel lesen …
… siehe unter => Scheitelpunktform der Parabelgleichung
… Abgrenzung unter => Parabel oder quadratische Funktion
… siehe unter => Scheitelpunktform
… siehe unter => Scheitelpunktform
