Mathematik
Dezimalpunkt, Tausendertrennpunkt und Multiplikations-Punkt: diese drei wichtigen Bedeutungen sind hier kurz erklärt. Viele weitere Bedeutungen stehen unter => Punkte
(Sub)Kultur
Die heutige Punk-Kultur wird erstmals in der Musikszene der 1970er greifbar Die Grundhaltung ist aggressiv, unversöhnlich, nonkonformistisch und illusionslos. Die ursprüngliche Punkszene Londons gab dem aussichtlosen Lebensgefühl von Jugendlichen einen Ausdruck. Prägend war auch der Anspruch, dass die Musik aus der Szene selbst heraus gemacht wurde, abseits des kommerziellen Konzert- und Plattengeschäfts. Der Aspekt der Trostlosigkeit und der Zurückgeworfenheit auf sich selbst lebte dann im neuen Jahrtausend unter anderem fort in der ästhetisierenden Kultur des => Cyberpunk
Liste verschiedener Bedeutungen
Tausenpunkt, Dezimalzpunkt, Schnittpunkt, 2D- oder 3D-Punkt, Wendepunkt etc.: das Wort Punkt hat sehr viele verschiedene Bedeutungen. Hier steht eine Liste dazu. => Ganzen Artikel lesen …
ist richtig geschrieben. Eine häufige Falschschreibung ist: puncto
… zum Beispiel (11|0), mehr dazu unter => Nullpunkt von Graphen
… so etwas wie (11|0), mehr dazu unter => Nullpunkt von Graphen
… es gibt mehrere Möglichkeiten, siehe => Steigung bestimmen
P(X1|Y1) und Q(X2|Y2): Steigung m = (Y2-Y1):(X2-X1)
Kennt man zwei Punkte in einem xy-Koordinatensystem, kann man daraus immer die (mittlere) Steigung m zwischen diesen zwei Punkten berechnen. Man dividiert dazu die Differenz der y-Werte durch die Differenz der x-Werte. Mehr dazu unter => Steigung aus zwei Punkten
… es gibt mehrere Möglichkeiten, siehe => Steigung bestimmen
 2D-Punkt
2D-Punkt
(5|3)
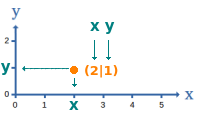
(5|3) ist eine typische Angabe für einen Punkt in einem xy-Koordinatensystem. Da ein xy-Koordinatensystem zweidimensional ist, kann man den Punkt auch einen 2D-Punkt nennen. Hier ist erklärt, was ein solcher Punkt anschaulich bedeutet. => Ganzen Artikel lesen …
… für x- und y-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
 2D-Punkt aus Koordinatensystem
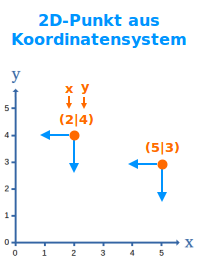
2D-Punkt aus Koordinatensystem
Anleitung
Man hat einen Punkt in einem xy-Koordinatensystem. Wenn man von dem Punkt aus direkt auf die x-Achse zeigt, kann man dort den x-Wert ablesen. Zeigt man direkt auf die y-Achse, kann man dort den y-Wert ablesen. Das wird hier kurz erklärt. => Ganzen Artikel lesen …
… für x- und y-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
… für x- und y-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen
… für x-, y- und z-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
… wie z. B. (4|2|Siehe unter => 3D-Punkt
 3D-Punkt
3D-Punkt
Definition
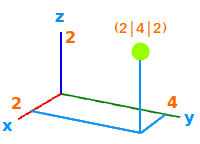
Einen Punkt in einem dreidimensionalen xyz-Koordinatensystem kann man als 3D-Punkt oder auch Raumpunkt bezeichnen. P(4|2|2) ist ein typisches Beispiel. Hier wird kurz erklärt, wie man solche Punkte schreibt und was die drei Zahlen, die Punktkoordinaten, anschaulich bedeuten. => Ganzen Artikel lesen …
 3D-Punkt aus Koordinatensystem
3D-Punkt aus Koordinatensystem
x, y und z ablesen
Ein Punkt in einem 3D-Koordinatensystem (xyz) ist gegeben. Man soll die x-, y- und z-Koordinaten bestimmen. Hier steht eine Schritt-für-Schritt Anleitung. => Ganzen Artikel lesen …
… für x-, y- und z-Werte, siehe unter => 3D-Punkt aus Koordinatensystem
… siehe unter => 3D-Punkt
… für x-, y- und z-Werte, siehe unter => 3D-Punkt aus Koordinatensystem
… wie z. B. (4|2|Siehe unter => 3D-Punkt
… für x-, y- und z-Werte, siehe unter => 3D-Punkt aus Koordinatensystem
Null Gravitationskraft
Man hat zwei Massen. Massen üben immer eine Anziehungskraft (Gravitationskraft) aufeinander aus. Der abarische Punkt ist ein Punkt genau zwischen den zwei Körpern, bei denen sich die Anziehungskräfte gegenseitig aufheben. => Ganzen Artikel lesen …
Technischer Fachbegriff [Bergbau]
Dort wo im Bergbau das Wertmineral abgebaut wird => Ganzen Artikel lesen …
Definition
Der Punkt an dem etwas den Boden verlässt und einen Flug beginnt. Das Wort wird zum Beispiel beim Starten von Flugzeugen und Raketen sowie auch mit Skischanzen verwendet. In der Physik spielt er eine Rolle beim Thema => waagrechter Wurf
… steht unter => Steigung in einem Punkt
… z. B. f'(4), siehe unter => Steigung in einem Punkt
… für x- und y-Werte, siehe unter => 2D-Punkt aus Koordinatensystem
… für x-, y- und z-Werte, siehe unter => 3D-Punkt aus Koordinatensystem
… Koordinaten ablesen, siehe unter => Punkte aus Koordinatensystem
… die höchsten Punkte in einem Intervall => globale Extrempunkte
… erste Ableitung und Randverhalten, mehr unter => Globalen Extrempunkt berechnen
… erste Ableitung und Randverhalten, mehr unter => Globalen Extrempunkt berechnen

