Proportionalität
Definition
Zwei Größen sind zueinander proportional, wenn der Wert der einen Größe geteilt durch den Wert der anderen Größe immer dasselbe Ergebnis gibt. Das übliche Zeichen für Proportionalität ist die Tilde ~. Sind zwei Größen zueinander proportional, dann gilt zum Beispiel auch die Dreisatzrechnung. => Ganzen Artikel lesen …
Proportionalitäten
Beispiele
Proportionalität heißt: man hat zwei Dinge und immer wenn das eine doppelt so groß wird wie es vorher war, dann wird auch das andere doppelt so groß wie es vorher war. Dazu hier einige Beispiele. => Ganzen Artikel lesen …
Mathematik
1 und 6, 2 und 3, 4 und 1,5: zwei Größen sind zueinander indirekt proportional, wenn ihr Produkt (Malrechnung) immer dasselbe Ergebnis ergibt. Das ist ausführlich erklärt im Artikel => umgekehrte Proportionalität
… meint in der Statistik dasselbe wie => Verhältnisskala
… siehe unter => Versuch Würfelproportionalität
… in der Mathematik dasselbe wie die => Antiproportionalitätskonstante
Mathematik
Bei einer antiproportionalen Zuordnung oder Funktion, auch umgekehrt proportional genannt, ergeben zwei einander zugeordnete Zahlen malgerechnet immer dasselbe Ergebnis. Man spricht auch von Produktgleichheit. Dieses immer gleiche Produkt ist die Antiproportionalitätskonstante. Das ist hier mit einem Beispiel kurz vorgestellt. => Ganzen Artikel lesen …
… Methoden und Aufgaben unter => Proportionalität erkennen über Tabellen
Mathematik
Man unterscheidet bei Zuordnungen und Funktionen eine direkte und eine indirekte (auch umgekehrte oder anti) Proportionalität. Die direkte Proportionalität gilt dann, wenn man die eine Größe verdoppeln kann und sich die andere dann immer auch verdoppelt. Diese direkte Proportionalität nennt man meist einfach auch nur => Proportionalität
Mathematik
1 und 24, 2 und 12, 3 und 8, 4 und 6: zwei Größen sind zueinander indirekt proportional, wenn ihr Produkt (Malrechnung) immer dasselbe Ergebnis ergibt. Das ist ausführlich erklärt im Artikel => umgekehrte Proportionalität
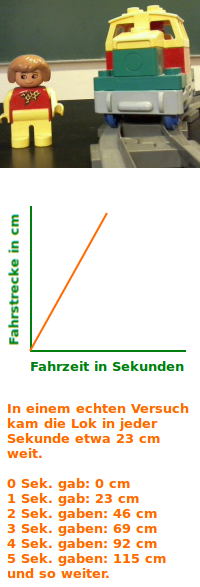Proportionalität erkennen
Anleitung
Hier werden verschiedene Methoden vorgestellt, wie man überprüfen kann, ob zwei Größen zueinander proportional sind. Was eine Größe in der Mathematik ist und wie proportional definiert ist steht auf der Seite => proportional
Wie man an Tabellen überprüft, ob zwei Größen proportional sind
Die folgenden zwei Methoden eignen sich für alle Tabellen mit zwei Zeilen (waagrecht) oder zwei Spalten (senkrecht). Hier ist eine waagrechte Beispieltabelle: => Ganzen Artikel lesen …
Wie man an Tabellen überprüft, ob zwei Größen proportional sind
Die folgenden zwei Methoden eignen sich für alle Tabellen mit zwei Zeilen (waagrecht) oder zwei Spalten (senkrecht). Hier ist eine waagrechte Beispieltabelle: => Ganzen Artikel lesen …
… wie das geht steht unter => Proportionalität erkennen über Tabellen
… Methoden und Aufgaben unter => Proportionalität erkennen über Tabellen
… Methoden und Aufgaben unter => Proportionalität erkennen über Tabellen
… Methoden und Aufgaben unter => Proportionalität erkennen über Tabellen
… Methoden und Aufgaben unter => Proportionalität erkennen über Tabellen
Konstante
In der proportionalen Zuordnung oder Funktion y=a·x nennt man die Zahl a den Proportionalitätsfaktor [1] oder auch die => Proportionalitätskonstante
Proportionalitätskonstante
Anschaulich
y=a·x oder kurz auch y=ax steht für eine sogenannte proportionale Funktion oder Zuordnung. Die Zahl a ist die Proportionalitätskonsten, oft auch Proportionalitätsfaktor [1] genannt. Diese Konstante kann man berechnen, wenn man eine y-Zahl durch die zu ihre gehörende x-Zahl teilt. Das ist hier näher erklärt. => Ganzen Artikel lesen …
∝ oder ~
Das ∝ leitet sich aus dem mittelalterlich-lateinischen æ als Abkürzung für aequalis ab, was so viel bedeutet wie Gleichheit. Heute steht das Zeichen genauso wie die Tilde ~ für die Idee der => Proportionalität
… erklärte Textbeispiele unter => wächst quadratisch mit
Mathematik
1 und 60, 2 und 15, 3 und 20, 4 und 15, 5 und 12, 6 und 10: zwei Größen sind zueinander indirekt proportional, wenn ihr Produkt (Malrechnung) immer dasselbe Ergebnis ergibt. Das ist ausführlich erklärt im Artikel => umgekehrte Proportionalität
… Methoden und Aufgaben unter => Proportionalität erkennen über Tabellen
Mathematik
=> Ganzen Artikel lesen …
Versuch Würfelproportionalität
Stochastik
Erzielt man mit einer doppelten Anzahl von Würfeln auch doppelt so viele Sechser? Dieser Frage geht der folgende Versuch nach. => Ganzen Artikel lesen …
