2: Potenzterme

… alle Terme der Form ax^r, Definition unter => Potenzterm

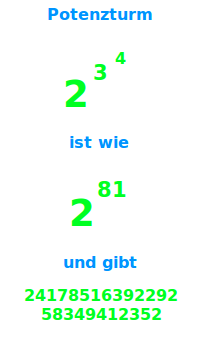
Potenzturm

2 hoch 3 hoch 4

2 hoch 3 hoch 4 ist ein Potenzturm. Entgegen der normalen Regel, dass man von links nach rechts rechnet, berechnet man einen Potenzturm von rechts nach links, also von oben nach unten. 2 hoch 3 hoch 4 gibt vereinfacht also 2 hoch 81. Das ist hier mit Zahlen kurz erklärt. => Ganzen Artikel lesen …

5: Funktion aus Potenztermen plus Zahl

… ist am ehesten eine => ganzrationale Funktion

6: Potenzterm durch Potenzterm

… wie etwa 2^5 durch Siehe unter => Potenz durch Potenz

Potenzterm in Wurzelterm

Umwandlung

Jeder Potenzterm kann auch als Wurzelterm geschrieben werden. Hier steht eine kurze Anleitung dazu. => Ganzen Artikel lesen …

8: Potenzterm mal Potenzterm

… wie etwa 2³ mal Siehe unter => Potenz mal Potenz

9: Potenzterme dividieren

… wie etwa 2^5 durch Siehe unter => Potenz durch Potenz

10: Potenzterme durch rechnen

… wie etwa 2^5 durch Siehe unter => Potenz durch Potenz

11: Potenzterme malnehmen

… wie etwa 2³ mal Siehe unter => Potenz mal Potenz

12: Potenzterme multiplizieren

… wie etwa 2³ mal Siehe unter => Potenz mal Potenz

13:

Wurzelterm in Potenzterm

Umrechnung

Die n-te Wurzel von x ist dasselbe wie x hoch 1/n. Diese Umrechnung wird bei vielen Termumformungen nützlich. Sie ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …

14: Wurzelterm in Potenzterm umwandeln

… √x = x^½, mehr unter => Wurzelterm in Potenzterm