Lernwerkstatt
Werkstattversuche, die zu einer Potenzgleichung führen: hier stehen Beispiele mit Anleitungen dazu. => Ganzen Artikel lesen …
x in der Basis
Als Potenzgleichung bezeichnet man jede Gleichung, die man umformen kann in a=x^r, also a gleich x hoch r. Steht statt dem a ein f(x), so handelt es sich um eine Potenzfunktion. => Ganzen Artikel lesen …
Versuch
Definition
Von einem Versuch spricht man, wenn a) wenn ein gewünschtes Ergebnis herbeigeführt werden soll, wobei der Erfolg aber unsicher ist und b) wenn überprüft werden soll, ob eine bestimmte Situation immer auch einen bestimmten daran geknüpften Folgezustand hat. Die Übergänge zum Begriff Experiment sind dabei fließend. => Ganzen Artikel lesen …
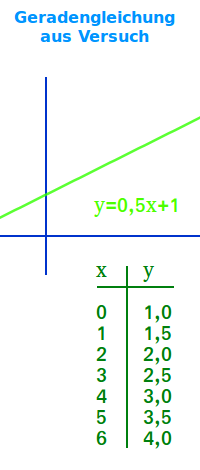Geradengleichung aus Versuch
Lernwerkstatt
Hier stehen mehrere einfach mit Haushalts- oder Baumarktmaterialien durchführbare Versuche zum Schulstoff der Mathematik aus den Klassen 6 bis 9. Es geht immer darum, eine Geradengleichung, zum Beispiel in der Form y=mx+b aufzustellen. Gesucht ist also immer die Gleichung einer linearen Funktion. Die Versuche wurden seit 2010 in der Mathe-AC Lernwerkstatt in Aachen entwickelt und sind seitdem häufig im Einsatz. Profis mit viel Routine gelingt es, die Gleichung ganz ohne die Verwendung von Notizen, also nur im Kopf, aufzustellen und dabei auch die Form des Graphen genau zu beschreiben. => Ganzen Artikel lesen …
Gleichung aus Versuch
… siehe unter => Funktionsgleichungen aus Versuchen
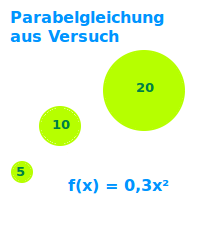Parabelgleichung aus Versuch
Lösungsidee und Beispiele
Wie hängt die Dauer einer Pendelschwingung von der anfänglichen Auslenkung ab? Es ist für viele ein verblüffendes Ergebnis: gar nicht - die Pendeldauer ist eine konstante Funktion der Auslenkung. Hier stehen einige Versuche, deren Auswertung zu einer konstanten Funktion führt. => Ganzen Artikel lesen …
Lernwerkstatt
Jede Gleichung, die als Graph eine Exponentialkurve hat. Jede Gleichung, die man in die Form y=a·c^[T(x)] bringen kann. T(x) meint hier: irgendein Term, in dem mindestens ein x vorkommt. Jede Gleichung, die man auch als Exponentialfunktion deuten kann. Hier stehen praktische Versuche dazu. => Ganzen Artikel lesen …
