Polstellen bestimmen
Verfahren, wie man Polstellen bestimmt
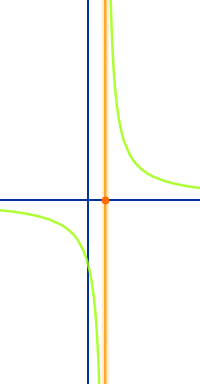
Polstellen treten normalerweise bei Funktionen auf, bei denen das x im Nenner steht. Um Polstellen zu finden, setzt man den (oder die) Nenner einer Funktionsgleichung gleich Null. Alle x-Werte, die den Nenner zu Null machen, können Polstellen sein. Wenn die Beträge der Funktionswerte in der Nähe dieser Werte dann in Richtung unendlich wachsen, dann liegt dort wirklich eine Polstelle vor. => Ganzen Artikel lesen …
Mathematik
Polstellen von Graphen einer Funktion f(x) sind Definitionslücken an denen der Graph sich an eine senkrechte Gerade asymptotisch annähert. Hier stehen Beispiele dazu. => Ganzen Artikel lesen …
Bestimmen
(Irgendwie) herausfinden
Bestimmen heißt: etwas herausfinden, wobei der genaue Weg dazu aber offen gelassen wird. Man kann etwas über eine Berechnung, über Schätzen, über Recherchieren oder sonstwie bestimmen. => Ganzen Artikel lesen …
Nullstellen bestimmen
Übersicht
ABC-Formel, pq-Formel, faktorisieren, graphisch oder über Substitution: du hast vielleicht schon einige Verfahren kennen gelernt und gemerkt, dass man hier leicht den Überblick verliert. Hier stehen die wichtigsten Methoden mit einigen Tipps als Übersicht. => Ganzen Artikel lesen …
Anleitung
Die Hochstelle ist eine Stelle auf der x-Achse. Sie ist der x-Wert, der zu einem Hochpunkt gehört. Um eine Hochstelle zu bestimmen, bestimmt man also einen Hochpunkt und nimmt davon nur den x-Wert. Das ist erklärt unter => Hochpunkte bestimmen
… x-Wert eines Sattelpunktes, mehr unter => Sattelstelle bestimmen
