Anleitung
Eine Ebene ist eine flache, gerade Fläche in einem 3D-Raum. Sie ist unendlich ausgedehnt, hat also keine Ränder. Um sie eindeutig zu definieren, kann man (irgend)einen Punkt auf der Ebene angeben. Das ist der Stützpunkt. Dann gibt man zwei (fast) beliebige Vektoren an, zu denen die Ebene parallel sein soll. Das sind die zwei Richtungsvektoren. Mit diesen Angaben ist die Ebene eindeutig definiert. => Ganzen Artikel lesen …
Vektorrechnung
In der Vektorrechnung, auch lineare Algebra oder analytische Geometrie genannt, kann man Geraden und Ebenen mit Hilfe von Parametern und Vektoren angeben. Siehe als Einstieg in das Thema die => Parameterform der Geraden
Ebene
Erdkunde, Mathematik
Als Landschaft ist eine Ebene eine große und weitgehend flache Landschaft ohne Hügel, Berge oder Senken. In der Mathematik ist eine Ebene eine Fläche, in die man in jeder Richtung vollständig Geraden hineinlegen kann. => Ganzen Artikel lesen …
Drei
1+1+1
Das Wort drei kommt in ähnlicher Form (tri) in vielen verschiedene Sprachen vor. In der Geometrie wird die Drei oft durch Silben wie kubisch oder Kubik angedeutet. => Ganzen Artikel lesen …
Anleitung
Zwei Punkte in einem xyz-Koordinatensystem sind gegeben. Daraus soll eine Gleichung mit Stütz- und Richtungsvektor erstellt werden, also eine Geradengleichung in Parameterform. Das ist hier erklärt. => Ganzen Artikel lesen …
… siehe unter => Parameterform der Ebene
… mit Vektoren, siehe unter => Parameterform der Geraden
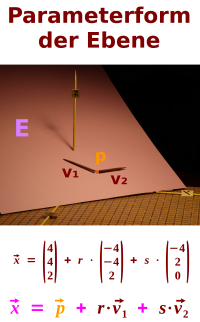Parameterform der Ebene
Vektorrechnung
E: x = p + r mal v1 + s mal v2: p ist der Stützvektor und v1 und v2 sind die zwei Richtungsvektoren: wie diese Gleichung eine Ebene im Raum beschreibt, ist hier kurz erklärt. => Ganzen Artikel lesen …
