Parameterform der Ebene
Vektorrechnung
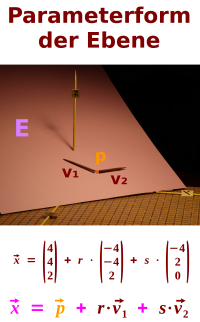
E: x = p + r mal v1 + s mal v2: p ist der Stützvektor und v1 und v2 sind die zwei Richtungsvektoren: wie diese Gleichung eine Ebene im Raum beschreibt, ist hier kurz erklärt. => Ganzen Artikel lesen …
Vektorrechnung
In der Vektorrechnung, auch lineare Algebra oder analytische Geometrie genannt, kann man Geraden und Ebenen mit Hilfe von Parametern und Vektoren angeben. Siehe als Einstieg in das Thema die => Parameterform der Geraden
Ebene
Erdkunde, Mathematik
Als Landschaft ist eine Ebene eine große und weitgehend flache Landschaft ohne Hügel, Berge oder Senken. In der Mathematik ist eine Ebene eine Fläche, in die man in jeder Richtung vollständig Geraden hineinlegen kann. => Ganzen Artikel lesen …
Parameterform der Geraden
Vektorrechnung
x=p+r·u ist die Kurzversion. Sie bedeutet: ein Ortsvektor zu eine beliebigen Punkt auf der Geraden = Stützvektor + r mal Richtungsvektor. Dies ist eine Art, Geraden in einem 2D sowie vor allem auch in einem 3D-Koordinatensystem anzugeben. Die Parameterform der Geraden spielt eine wichtige Rolle in der sogenannten Vektorrechnung (lineare Algebra, analytische Geometrie). Hier wird erklärt, was diese Form einer Geradengleichung anschaulich darstellt. => Ganzen Artikel lesen …
Vektorrechnung
Bei einer sogenannten Normalenform der Ebene gibt man genau einen Punkt der Ebene an, den Stützpunkt. Die Ebene muss also durch diesen Punkt gehen. Sie hat dann aber noch unendlich viele Möglichkeiten, wie sie im Raum orientiert ist. Wenn man dann aber noch einen Vektor angibt, zu dem den Ebene senkrecht (das heißt normal) stehen soll, also auch einen 90°-Winkel bildet, dann gibt es nur noch genau eine Ebene, die auf diese Angaben passt. Diese Grundidee der Normalenform führt dann zu verschiedenen => Normalenformen der Ebene
… siehe unter => Normalenform der Ebene
… siehe unter => Parameterform der Ebene
Anleitung
Eine Ebene ist eine flache, gerade Fläche in einem 3D-Raum. Sie ist unendlich ausgedehnt, hat also keine Ränder. Um sie eindeutig zu definieren, kann man (irgend)einen Punkt auf der Ebene angeben. Das ist der Stützpunkt. Dann gibt man zwei (fast) beliebige Vektoren an, zu denen die Ebene parallel sein soll. Das sind die zwei Richtungsvektoren. Mit diesen Angaben ist die Ebene eindeutig definiert. => Ganzen Artikel lesen …
