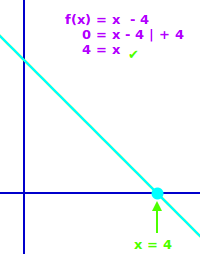
Nullstellen von Geraden berechnen
Übersicht
y = 4x-20 hat als Nullstelle die Zahl 5 auf der x-Achse: eine Nullstelle ist der x-Wert, bei dem die Gerade die x-Achse schneidet. Für die Berechnung gibt es ein Verfahren, das immer funktion, nämlich umformen oder umstellen nach x. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Nullstellen
Beispiele
Nullstellen sind x-Werte auf der x-Achse, bei denen ein Funktionsgraph die x-Achse schneidet. Hier sind Beispiele für z. B. Geraden, Parabeln, Kubische, ganzrationale und einige andere Funktionstypen. => Ganzen Artikel lesen …
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
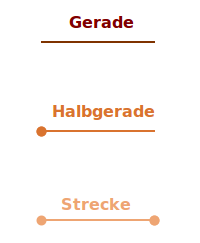Geraden
In der Mathematik: Klassifizierung und Arten
In der Mathematik werden Geraden sowohl innerhalb der Geometrie (2D und 3D) als auch in der Funktionen- und Gleichungslehre behandelt. In der Anylsis spielen sie als Veranschaulichung von linearen Funktionen (Geradengleichung) eine grundlegende Rolle. Es folgen jetzt verschiedene Typen von Geraden. => Ganzen Artikel lesen …
Berechnen
Definition
Bis auf einen Zahlenwert genau bestimmen. Man kann zum Beispiel den Gesamtpreis von 4 Äpfeln berechnen, wenn man weiß, dass jeder einzelne Apfel 50 Cent kostet. Man rechnet: 4 mal 50 Cent und hat als Gesamtpreis dann 200 Cent oder genau 2 €. => Ganzen Artikel lesen …
… gerechnetes Beispiel unter => Nullstellen von Geraden berechnen
… gerechnetes Beispiel unter => Nullstellen von Geraden berechnen
… gerechnetes Beispiel unter => Nullstellen von Geraden berechnen
… siehe unter => Nullstellen von Geraden berechnen
