Anleitung
Die Nullfunktion f(x)=0 aufgeleitet gibt F(x)=0+C. Das große C ist die sogenanne Integrationskonstante und steht für eine beliebge Zahl, die man sich aussuchen kann. Jeder Funktion F(x)=Zahl ist abgeleitet f(x)=0 und ist daher eine Stammfunktion von f(x). => Ganzen Artikel lesen …
 Nullfunktion
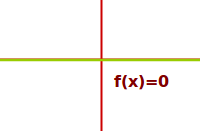
Nullfunktion
f(x)=0
Ordnet jedem x-Wert die Zahl 0 als Funktionswert zu. Der Graph ist identisch mit der x-Achse. => Ganzen Artikel lesen …
F(x) bestimmen
Definition: Als Aufleiten bezeichnet man die Bestimmung einer Stammfunktion F(x) zu einer gegebenen Funktion f(x). Das Aufleiten ist die Gegenoperation des Ableitens: f(x) aufgeleitet gibt F(x). Und F(x) abgeleitet gibt f(x). Hier werden kurz Verfahren dazu vorgestellt. => Ganzen Artikel lesen …
 Nullfunktion ableiten
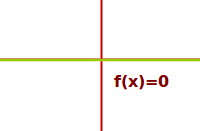
Nullfunktion ableiten
f(x)=0 ergibt abgeleitet f'(x)=0
Die Nullfunktion hat als Graphen sozusagen die x-Achse. Der Graph verläuft überall waagrecht und hat damit auch für alle x-Werte die Steigung 0. Entsprechend muss die Ableitungsfunktion für alle x-Werte die Zahl 0 ergeben. Es gilt also f(x)=0 ergibt abgeleitet f'(x)=0. => Ganzen Artikel lesen …
Kurze Anleitung
Eine Funktion der Form f(x) = e hoch irgendetwas mit x nennt man eine e-Funktion. Für einige einfache Fälle gibt es Aufleitungsregeln, für andere kennt man noch keine. => Ganzen Artikel lesen …
F(x) = x
Die Einsfunktin f(x) = 1 aufgeleitet gibt ihre Stammfunktin F(x) = x + C. Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
… also von f(x)=0, steht unter => Nullfunktion ableiten
… also von f(x)=0, steht unter => Nullfunktion ableiten

