 Mittelwert von Funktionswerten über Integral
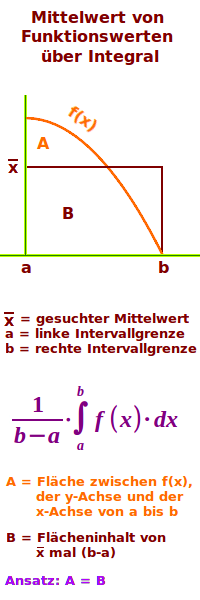
Mittelwert von Funktionswerten über Integral
Durchschnitt von f(x) = ?
Man hat einen Funktion mit Graphen gegeben und sucht das arithmetische Mittel der Funktionswerte (y-Werte). Arithmetisches Mittel ist hier dasselbe wie der Durchschnitt. Eine oft einfache Rechenmethode bietet der => Mittelwertsatz der Integralrechnung
Statistik
Mittelwert ist ein Überbegriff. Zu den Mittelwerten gehören zum Beispiel der Median, Durchschnitt oder das geometrische Mittel. Mittelwert an sich steht oft für das arithmetische Mittel. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
 Über
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
∫: Definition
Das bestimmte Integral ist immer ein einzelner Zahlenwert. Ein unbestimmtes Integral hingegen ist eine Funktion. Neben dieser mathematischen Deutung heißt das Adjektiv integral auch so viel wie der wesentliche Teil von einem größeren Ganzen [1]. Hier wird die mathematische Bedeutung des Wortes Integral erklärt. => Ganzen Artikel lesen …
… Anleitung unter => Mittelwert von Funktionswerten über Integral
… Anleitung unter => Mittelwert von Funktionswerten über Integral
 Mittelwert von Funktionswerten
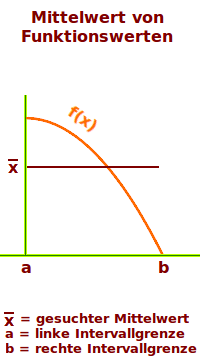
Mittelwert von Funktionswerten
Arithmetisches Mittel
Man hat den Graphen einer Funktion, etwa eine nach unten geöffnete Parabel, wie von der Funktion f(x)-x²+1. Man kann nun alle Funktionswerte (es sind unendlich viele) zwischen zwei Punkten des Graphen betrachten. Wie könnte man ihren Mittelwert, also ihren Durchschnitt berechnen? Eine Lösung ist hier kurz vorgestellt. => Ganzen Artikel lesen …

