… zusammengedacht alle => komplexe Zahlen
Menge
Definition
Eine Menge in der Mathematik ist eine beliebige Zusammenstellung verschiedener Dinge. Die Dinge dürfen - müssen aber nicht - geordnet sein. Jedes Ding, man spricht von Elementen, darf dabei nur genau einmal vorkommen. Das wird hier erläutert. => Ganzen Artikel lesen …
… Brüche, Dezimalzahlen, Kommazahlen etc. => Zahlenarten
Beispiele
Jede Zahl, die man sich als einen Punkt in der Gaußschen Zahlenebene vorstelellen kann ist komplexe. Ein mathematisches Objekt, mit dem das nicht geht ist keine komplexe Zahl, man scheibt formal: x ∉ ℂ. Hier stehen einige Objekte, die keine komplexe Zahlen sind. => Ganzen Artikel lesen …
… zusammengedacht alle => reelle Zahlen
… ℤ als Menge aller ganzen Zahlen zusammengedacht => ganze Zahlen
x ∈ ℂ
x ∈ ℂ heißt: man darf für x jede komplexe Zahl einsetzen, aber auch nur solche. Da jede reelle Zahl auch eine komplexe Zahl ist, sind sie jedoch mit eingeschlossen. Das ist hier weiter erklärt. => Ganzen Artikel lesen …
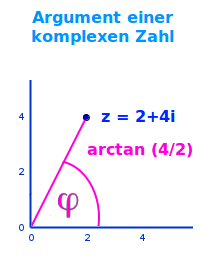Argument einer komplexen Zahl
Definition
Das Argument einer positiven Zahl ist ein Winkel in einer Gaußschen Zahlenebene, die der Visualisierung der komplexen Zahl dient. Das ist hier Schritt-für-Schritt erklärt. => Ganzen Artikel lesen …
