Geometrie
Ein Lot, Lotlinie [1] oder auch Schwerelinie [3] bezeichnete ursprünglich eine Linie in Richtung der Schwerkraft. Die Lotlinie oder Lotgerade ging damit senkrecht nach unten und senkrecht nach oben. Später wurde der Begriff verallgemeinert. Heute steht Lotgerade in der Geometrie für jede Gerade, die mit einem Winkel von 90° auf ein anderes Objekt trifft oder dieses schneidet [1]. Zu dieser Bedeutung im Sinne der Geometrie siehe den Artikel => Lot (Mathematik)
xy-Koordinatensystem
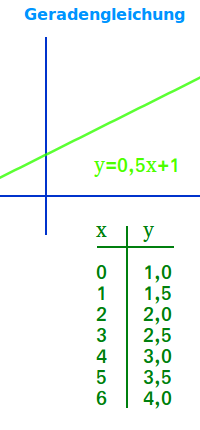
y = 4x+2 - das ist die Gleichung einer typischen Gerade in einem xy-Koordinatensystem, also in einem zweidimensionalen oder kurz 2D-Koordinatensystem. Dazu hier mehr zur Definition. => Ganzen Artikel lesen …
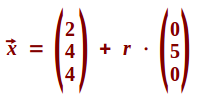3D-Gerade
Gerade in ein einem 3D-Koordinatensystem
Eine Gerade in sich ist ein eindimensionales Gebilde: man kann sich auf ihr nur hin und her bewegen, in einer Dimension. Betrachtet man die Gerade aber als platziert in einem dreidimensionalen Koordinatensystem, kann man sie als 3D-Gerade bezeichnen. => Ganzen Artikel lesen …
Gerade
Übersicht
Eine Gerade in der Mathematik ist eine Linie ohne Ecken, Lücken, Kurven oder Enden: sie ist unendlich lang gedacht. Die kürzeste Verbindung zwischen zwei Punkten liegt immer auf einer Geraden. Hier werden Geraden in verschiedenen Teilgebieten der Mathematik kurz vorgestellt. => Ganzen Artikel lesen …
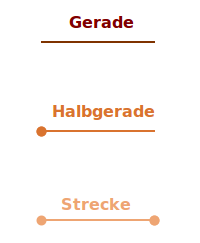Geraden
In der Mathematik: Klassifizierung und Arten
In der Mathematik werden Geraden sowohl innerhalb der Geometrie (2D und 3D) als auch in der Funktionen- und Gleichungslehre behandelt. In der Anylsis spielen sie als Veranschaulichung von linearen Funktionen (Geradengleichung) eine grundlegende Rolle. Es folgen jetzt verschiedene Typen von Geraden. => Ganzen Artikel lesen …
360°
Als Altgrad bezeichnet man die klassische - das heißt übliche und normale - Einteilung des Kreises in 360 Grad. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
