Logisches UND
Alle Aussagen sind wahr
Das logische UND verbindet zwei oder mehr Teilaussagen zu einer neuen Gesamtaussage. Diese Gesamtaussage ist genau dann wahr, wenn alle vorherigen Teilaussagen wahr waren. In jedem anderen Fall ist die mit UND erzeugte Gesamtaussage falsch. => Ganzen Artikel lesen …
Logisches UND
x=3 UND x=4 heißt: x soll gleichzeitig 3 und 4 sein. Das ist ein logischer Widerspruch. Besser ist oft das logische ODER: Möchte man beispielweise als zwei Lösungen einer pq-Formel angeben, dass einmal x=3 und einmal x=4 als Lösung gilt, dann schreibt man: x=3 ODER x=4; kurz: x=3 v x=4. Lies mehr unter => Logisches UND
Δ, δ, ∂
Δ, δ, ∂ sind verschiedene Schreibweisen des griechischen Buchstaben d, ausgesprochen als Delta. Das Delta spielt eine herausragende Rolle in der Mathematik und Physik. Es steht oft für die Idee eines Unterschiedes (Differenz). Hier steht eine kurze Übersicht. => Ganzen Artikel lesen …
ν, Ν, ℕ
ν, Ν, ℕ sind verschiedene Varianten des lateinischen und griechischen Buchstaben N. Sie spielen unter anderem in der Mathematik und Physik eine Rolle. Hier stehe eine kurze Übersicht. => Ganzen Artikel lesen …
∩, ∪, ν, υ, μ, û
∩, ∪, ν, υ, μ, û sind Varianten des lateinische Buchstaben U und des griechischen Nü oder Ny. Sie werden unter anderem in der Mathematik und Physik verwendet. Hier steht eine kurze Übersicht zu besonders wichtigen Schreibweisen. => Ganzen Artikel lesen …
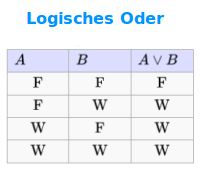Logisches ODER
Mindestens eine Aussage ist wahr
Das logische ODER verbindet zwei oder mehr Teilaussagen zu einer neuen Gesamtaussage. Diese Gesamtaussage ist genau dann wahr, wenn mindestens eine der vorherigen Teilaussagen wahr war. => Ganzen Artikel lesen …
… in der Aussagenlogik, siehe unter => Logisches Nicht
Logisches Nicht
¬ Verneinung
Das logische Nicht steht für die Verneinung einer Aussage, also die Formulierung einer Art Gegenteil einer Aussage. Das wird an einem Beispiel aus der Geometrie kurz erklärt. => Ganzen Artikel lesen …
