 Logarithmus
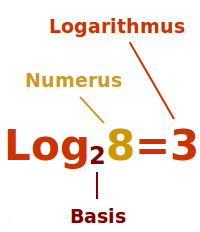
Logarithmus
Definition
2 hoch was gibt 8? Die Antwort 3 ist auch der Logarithmus. Ein Logarithmus ist eine Hochzahl, die aus einer gegebenen Basis einen gewünschten Potenzwert erzeugt. In der Zeit bevor es Rechenmaschinen gab, erleicherte der Logarithmus den Rechenaufwand erheblich. [1] Das ist hier näher erklärt. => Ganzen Artikel lesen …
… Grundtyp gibt 1 durch x·ln(Basis) => Logarithmusfunktion ableiten
Definition
Das Wort wird in der Mathematik nicht einheitlich verwendet. Zum einen steht es für jede Gleichung, die einen Logarithmus-Term enthält. In einem engeren Sinn steht es nur für Gleichungen, bei denen die Unbekannte im Numerus steht. Beides ist hier kurz vorgestellt. => Ganzen Artikel lesen …
 Logarithmusrechnung
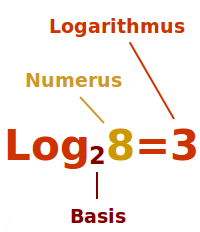
Logarithmusrechnung
Übersicht
Grundlegende Begriffe und Definitionen werden kurz vorgestellt. Die Logarithmusrechnung ist sozusagen das Potenzrechnen umgekehrt gedacht. => Ganzen Artikel lesen …
… Beispiele unter => Logarithmenbasen
… für die Zahlenwerte siehe => Logarithmen
… ln(x) abgeleitet gibt 1/x oder x^(-1) => Logarithmusfunktion ableiten
… ln(x) abgeleitet gibt 1/x oder x^(-1) => Logarithmusfunktion ableiten
… ist ist nicht definiert (gibt es nicht), Kurzerklärung unter => lg 0
… ln(x) abgeleitet gibt 1/x oder x^(-1) => Ableitungsregeln
… ln(x) abgeleitet gibt 1/x oder x^(-1), siehe auch => Ableitungsregeln
… Beispiele unter => Logarithmenbasen
… Logagrithmus zur Basis 2, siehe unter => Binärer Logarithmus
… mit der Basis e, heißt auch => natürlicher Logarithmus
ist ist nicht definiert.
ist ist nicht definiert.
ist genau 0.
… ln(x) abgeleitet gibt 1/x oder x^(-1)
ist genau 2.
ist genau 0.
… ln(x) abgeleitet gibt 1/x oder x^(-1)
ist ist nicht definiert.
ist ist nicht definiert.
ist genau 0.
ist genau 2.
ist genau 1.
ist genau 0.
ist genau 2.
ist ist nicht definiert.
… ln(x) abgeleitet gibt 1/x oder x^(-1)
… siehe unter => Logarithmus von Null
ist genau 1.
ist genau 0.
ist genau 2.
… Funktionsgleichung und Infos unter => f[x]=ln[x]

