Anleitung
Kein besonderes Gesetz: Logarithmen einzeln ausrechnen, dann teilen. Das ist hier kurz mit Zahlenbeispielen vorgestellt. => Ganzen Artikel lesen …
Beispiele
lg ⭢ hat als Basis die Zahl 10 (dekadischer Logarithmus), ln ⭢ hat die Basis e (natürlicher Logarithmus), und lb ⭢ hat als Basis die Zahl 2 (binärer Logarithmus). Hier stehen einige Zahlenbeispiele zu Logarithmen mit verschiedenen Basen. => Ganzen Artikel lesen …
 Basis
Basis
Mathematik
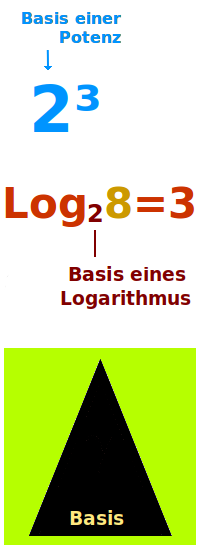
Als Basis bezeichnet man ganz allgemein Dinge, die unten sind. Bei der Potenz 2³ ist die Zahl 2 entsprechend die Basis, nämlich die Zahl, die unten steht. Von einer Basis spricht man zum Beispiel auch bei Logarithmen, Dreiecken, Trapezen, Geodreiecken, Vektoren oder ganzen Weltbildern. Das ist hier kurz mit Beispielen vorgestellt. => Ganzen Artikel lesen …
Rechenwege
Dividieren ist das Fremdwort für Teilen. Hier werden einige Rechenmethoden mit natürlichen Zahlen, Brüchen und Kommazahlen vorgestellt. => Ganzen Artikel lesen …
Anleitung
lg(100)+lg(10=lg(1000): lg steht für den Logarithmus mit der Basis 10. Bei lg(100) und lg(10) sind die Basen also beide die Zahl 10 und damit gleich. Sind die Basen gleich, werden lediglich die Numeri multipliziert. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Anleitung
Kein besonderes Gesetz: Logarithmen einzeln ausrechnen, dann potenzieren: das ist hier kurz mit einem Zahlenbeispiel vorgestellt. => Ganzen Artikel lesen …
Anleitung
Es gibt hierzu kein besonderes Gesetz: man muss die Logarithmen einzeln ausrechnen und dann multiplizieren. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… so etwas wie 2³:2² => Potenzen mit gleicher Basis dividieren

