Beispiele
4x = 20-x: hier stehen einige Beispiele und Gegenbeispiele zu linearen Gleichungen. Lineare Gleichungen können eine oder auch mehrere Unbekannte haben. => Ganzen Artikel lesen …
Gleichungen
Systematik
Lösbar, unlösbar, Identitäten, Funktionsgleichungen, lineare oder quadratische Gleichunen oder auch Reaktionsgleichungen in der Chemie: hier steht eine Übersicht nach verschiedenen Ordnungskriterien. Eine Gesamtübersicht zum Thema steht unter => Gleichungslehre
… Beispiele, was das ist => Lineare Gleichungen
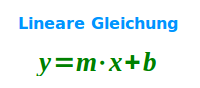Lineare Gleichung
Definition
Jede Gleichung, die man umformen kann in y = m·x+b nennt man linear. Wichtig ist, dass das x keine Hochzahl (außer der gedachten 1) hat und auch nicht in einem Nenner steht. Das ist hier näher erklärt. => Ganzen Artikel lesen …
Beispiele
Hier stehen einige beispielhafte Gleichungen mit Lösungen sowie ein Hinweis, wie man Gleichungen löst. => Ganzen Artikel lesen …
Verfahren
8=2x+2 hat die Lösung x=3. Eine lineare Gleichung kann eine oder zwei Unbekannte haben. Für beide Fälle gibt es eigene Lösungsverfahren, die hier kurz vorgestellt sind. => Ganzen Artikel lesen …
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
… siehe unter => Geradengleichung aufstellen
Anleitung
4x+18 = 2x+30 hat die Lösung x=6. Hier steht eine Schritt-für-Schritt Anleitung mit Praxisaufgaben im Übungsteil (qck). => Ganzen Artikel lesen …
z. B. 4·(x-5) = 12
Der erste Schritt ist meistens das Auflösen der Klammer. Im Beispiel oben ergäbe das 4x-20 = 12. Dann kann man weiter nach x umformen (ergäbe hier: x=8). Mehr dazu unter => lineare Gleichungen mit Klammern lösen
Beispiel
z. B. 4(2x+3)-8=28 kann zuerst über das Auflösen der Klammer vereinfacht werden. Anschließend kann die Gleichung durch Zusammenfassen und Umformen gelöst werden. Das ist hier Schritt-für-Schritt vorgestellt. => Ganzen Artikel lesen …
… siehe unter => Lineare Gleichungen mit zwei Unbekannten lösen
Bedeutung
y+x=10 ist eine lineare Gleichung mit zwei Unbekannten. Eine Lösung ist zum Beispiel das Zahlenpaar x=9 und y=1. Daneben gibt es noch unendlich viele weitere Lösungen. Das ist hier ausführlich erklärt. => Ganzen Artikel lesen …
… mehrere Methoden unter => Nullstellen von Geraden bestimmen
Beispiele
4x+8 = 2x+6 oder 12x-4 = 7x+21 oder auch 20+3x = 80 sind eher einfache lineare Gleichungen. Einfach heißt, dass zum Beispiel Brüche oder echte Kommazahlen fehlen. Mehr dazu unter => Sehr einfache lineare Gleichungen lösen
Tipps
6x-8 = 2x+20 ist eine eher einfache lineare Gleichung. Hier steht eine Anleitung, wie man sie lösen kann. Lösen heißt: eine Zahl finden, die für x engesetzt links und rechts vom Gleichzeitszeichen dasselbe Ergebnis gibt. Das ist hier erklärt. => Ganzen Artikel lesen …
so müsste es eigentlich heißen…
Man spricht normalerweise von linearen Gleichungssystemen. Das würde streng genommen bedeuten, dass das Gleichungssystem selbst linear wäre. Linearität ist aber keine mögliche Eigenschaft eines Gleichungssystems. Tatsächlich meint man, dass die einzelnen Gleichungen alle linear sind und dass man aus diesen linearen Gleichungen dann ein System baut: System linearer Gleichungen. Tatsächlich redet man aber von einem Linearen Gleichungssystem, oft abgekürzt als LGS. => Ganzen Artikel lesen …
