Lineare Funktionen

Beispiele

Linear nennt man jede Funktion, deren Gleichung man in die Form f(x)=ax+b oder f(x)=mx+b bringen kann. Der Graph einer linearen Funktion ist immer eine Gerade. Die Funktionsgleichung einer linearen Funktion ist immer eine Geradengleichung. Es folgen einige Arten und Beispiele. Eine Übersicht zum gesamten Thema steht auf => lineare Funktion

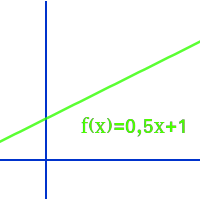Lineare Funktion

y=mx+b

Jede Funktion, deren Funktionsgleichung man in der Form f(x)=mx+b schreiben kann heißt linear. Der Graph einer linearen Funktion ist immer einer Gerade (aber nicht jede Gerade gehört zu einer linearen Funktion). Auf dieser Seite stehen wichtige Fachworte zu linearen Funktionen. => Ganzen Artikel lesen …

4: Lineare Funktionen NS

… Erklärungen und Aufgaben => Nullstellen von linearen Funktionen

6: NS linearer Funktionen

… Erklärungen und Aufgaben => Nullstellen von linearen Funktionen

7: Aus Texten lineare Funktionen aufstellen

… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text

8: Diskussion lineare Funktionen

… siehe unter => Lineare Funktionen Diskussion

10: Lineare Funktionen ablesen

… z. B. y=4x+8 aus Graph bestimmen => Geradengleichung aus Graph

11: Lineare Funktionen aufstellen

… z. B. aus Texten oder Punkten => Geradengleichung aufstellen

12: Lineare Funktionen aufstellen auf Versuchen

… z. B. y=mx+b, siehe unter => Geradengleichung aus Versuch

13: Lineare Funktionen aufstellen auf Versuchsen

… z. B. y=mx+b, siehe unter => Geradengleichung aus Versuch

14: Lineare Funktionen aufstellen aus Graph

… z. B. y=4x+8 aus Graph bestimmen => Geradengleichung aus Graph

15: Lineare Funktionen aufstellen aus Texten

… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text

16: Lineare Funktionen aus Graph aufstellen

… z. B. y=4x+8 aus Graph bestimmen => Geradengleichung aus Graph

17: Lineare Funktionen aus Text

… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text

18: Lineare Funktionen aus Texten

… Kurztipps und Aufgaben, siehe unter => Geradengleichung aus Text

20: Lineare Funktionen diskutieren

… siehe unter => Lineare Funktionen Diskussion

23: Lineare Funktionen graphisch bestimmen

… z. B. y=4x+8 aus Graph bestimmen => Geradengleichung aus Graph

24: Lineare Funktionen in Punktsteigungsform

… siehe unter => Punktsteigungsform der Geradengleichung

26: Lineare Funktionen Klassenarbeit

… Übersicht | Aufgaben | Lösungen => Lineare Funktion

27: Lineare Funktionen Kurvendiskussion

… siehe unter => Lineare Funktionen Diskussion

28: Lineare Funktionen Kurvendiskussionen

… siehe unter => Lineare Funktionen Diskussion

30: Lineare Funktionen Nullstelle

… siehe unter => Nullstellen von Geraden

31: Lineare Funktionen Nullstellen

… siehe unter => Nullstellen von Geraden

32: Lineare Funktionen Schnittpunkt bestimmen

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

33: Lineare Funktionen Schnittpunkte bestimmung

… Anleitung unter => Schnittpunkte von zwei Geraden graphisch bestimmen

34: Lineare Funktionen Schnittpunkte mit x-Achse bestimmen

… mehrere Methoden unter => Nullstellen von Geraden bestimmen

35: