Kugeldurchmesser
Definition
Eine Kugel hat außen eine Hülle, den Kugelrand. Wenn man gedanklich auf der Hülle startet, gerade durch die Mitte geht und dann auf der anderen Seite wieder bis zur Hülle weitergeht, dann hat man genau den Durchmesser abgelaufen. Man könnte auch sagen: der Kugeldurchmesser ist die längste gerade Strecke von einem Punkt auf der Kugeloberfläche zu einem anderen Punkt auf der Kugeloberfläche. Der Kugeldurchmesser ist immer doppelt so groß wie der Kugelradius. Übliche Abkürzungen sind ein großes D oder ein kleines d. => Ganzen Artikel lesen …
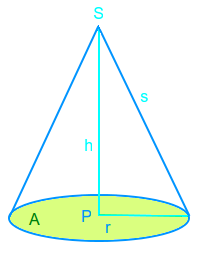Kegeldurchmesser
Definition
Als Kegeldurchmesser bezeichnet man den Durchmesser eines kreisförmigen Kegelbodens, auch Grundfläche genannt. Das ist hier kurz erläutert. => Ganzen Artikel lesen …
Außendurchmesser
Vom äußeren Rand, durch die Mitte bis wieder zum äußeren Rand
Der Außendurchmesser wird oft mit einem großen D abgekürzt (Innendurchmesser oft mit d). Der Außendurchmesser geht immer vom äußeren Rand eines kreisförmigen oder kugeligen Gebildes in gerader Linie durch die Mitte bis wieder zum äußeren Rand auf der gegenüberliegenden Seite. => Ganzen Artikel lesen …
Berechnung
Ein Ball hat normalerweise Kugelform. Der Durchmesser einer Kugel geht von der Kugeloberfläche durch die Kugelmitte bis - auf der anderen - Seite wieder auf die Kugeloberfläche. Da ein Ball eine Hülle hat und diese Hülle eine Dicke hat, kann man einen Innen- und Außendurchmesser unterscheiden. Lies mehr dazu unter => Kugeldurchmesser
Atomphysik
Die genauen Durchmesser der Atomkerne sind nicht exakt bekannt. Es gibt aber theoretisch ermittelte Schätzungen, im Sinn von hypothetische Durchmessern von Atomkernen. Hier wurden die Durchmesser unter folgenden zwei Annahmen berechnet: a) die Form der Atomkerne sei kugelig und b) die Dichte der Atomkerne sei 3 mal 10^(-17) kg/cbm. => Ganzen Artikel lesen …
… heißt in der Mathematik => Würfeldiagonale
d = 2·√(A:(4π))
Kugeloberfläche erst durch 4 teilen und das Ergebnis dann durch pi (etwa 3,14) teilen. Von diesem Ergebnis dann die Wurzel ziehen. Dann das Ergebnis noch mal zwei rechnen. Das Endergebnis ist dann der Kugeldurchmesser. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Geometrie
Radius mal 2 gibt Durchmesser: Wenn ein Kugel einen Radius von 4 Zentimeter hat, dann ist ihr Durchmesser 8 Zentimeter. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
d = U durch pi
Der Kugelumfang U ist gegeben und der Durchmesser d ist gesucht. Die Formel oben gibt die direkte Lösung. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
Anleitungen
Gegeben: Radius, Durchmesser, Umfang oder oder Oberfläche: man kann aus jeder dieser Angaben immer den Durchmesser berechnen. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
… messen, berechnen etc., siehe unter => Durchmesser bestimmen
Kugeldurchmesser messen
Tipp
Bei kleineren Kugeln kann man einen Messschieber, auch Schieblehre genannt, verwenden. Man legt die zwei Schenkel, deren gerade Seiten nach innen zeigen von außen an die Kugel an und liest dann den Messwert ab. Siehe auch => Messschieber
Anleitung
U = pi mal d: multipliziert man den Durchmesser einer Kugel mit der Kreiszahl pi (etwa 3,14) dann erhält man als Ergebnis den Umfang der Kugel. Beispiel: der Durchmesser der Erdkugel beträgt etwa 12756 km. Das multipliziert mit 3,14 gibt rund 40 Tausend Kilometer. Mehr unter => Kugelumfang berechnen
