Kreisring
Lochkreis
Ein Kreis mit einem Loch in der Mitte: ein Kreisring hat als Randlinien zwei Kreise: der innere Kreis muss dabei kleiner sein als der äußere Kreis. Zudem müssen die zwei Kreise konzentrisch sein. Konzentrisch meint, dass sie denselben Mittelpunkt haben. Der innere Kreis liegt also genau in der Mitte des äußeren Kreises. Siehe auch => konzentrisch
… ist in der Geometrie dasselbe wie ein => Torus
ist richtig geschrieben. Eine häufige Falschschreibung ist: kreiern
… wie langgezogener Kreis, ist am ehesten eine => Ellipse
… die Größe ist egal, aber die Form ist genau die von einem => Kreis
Kreislinie
Der Rand eines Kreises als Linie
Die Randlinie eines Kreises: die Kreislinie wird dabei so gedacht, als hätte sie keine Breite, also unendlich dünn. Ein anderes Wort für die Kreislinie ist => Kreisumfang
… siehe unter => Kreisringfläche berechnen
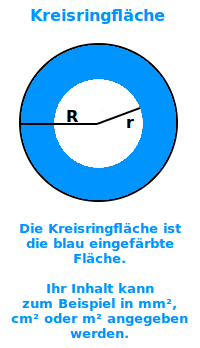Kreisringfläche
A = π·(R²-r²)
Legende: π ist die Kreiszahl pi (etwa 3,14). Groß R ist der Außen- und klein r ist der Innendurchmesser. Das Ergebnis kann man zum Beispiel angeben in cm² oder m². => Ganzen Artikel lesen …
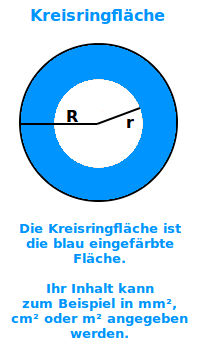Kreisringfläche berechnen
A = π·R²-π·r²
Ein Kreisring ist das, was übrig bleibt, wenn man von einer Kreisscheibe in der Mitte einen kleineren Kreis herausschneidet. Das Wort Kreisringfläche meint oft auch den Flächeninhalt dieses Kreises. Man kann ihn zum Beispiel angeben in cm² oder m². In diesem Artikel ist beschrieben, wie man diese Kreisringfläche A berechnet. => Ganzen Artikel lesen …
… zum Beispiel in cm², siehe unter => Kreisringfläche
Kreisringscheibe
Geometrie
Eine kreisförmige Scheibe mit Höhe und einem Loch in der Mitte: ein Kreisring ist eine flache 2D-Figur. Eine Kreisringscheibe ist eine 3D-Figur mit Höhe und Volumen. In der Geometrie ist sie identisch mit einem flachen Hohlzylinder. => Ganzen Artikel lesen …
… Besser => Torusvolumen
Das Wort Kreisring meint einen flach gedrückten Ring. Ein flacher Ring aus einer Papierseite ausgeschnitten wäre ein Kreisring. Mathematisch ist ein solcher Ring als unendlich flach gedacht. Volumen meint aber, wie viel Raum etwas braucht. Gedanklich meint das: wie viel Knete bräuchte man, um so einen Körper nachzukneten. Etwas ganz flaches aber bräuchte gar keine Knete zum nachformen, also hat es auch kein Volumen. Eine gut passende Alternative ist aber das Volumen einer Art Rettungsring. Lies mehr dazu unter => Torusvolumen
