 Kistendiagonale
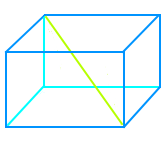
Kistendiagonale
Von Ecke durch Mitte zu Ecke
Eine Diagonale ist allgemein eine Strecke von einer Ecke eines Körpers oder einer Fläche zu einer gegenüberliegenden Ecke. Bei einer Kiste kann es mehrere Diagonalen, auch Quaderdiagonalen genannt, geben. => Ganzen Artikel lesen …
 Rautendiagonale
Rautendiagonale
Definition
Eine gerade Strecke von einer Ecke zur gegenüberliegenden Ecke in einer Raute. Als Raute bezeichnet man jedes Viereck, bei dem alle Seiten gleich lang sind. Das ist hier näher erklärt. => Ganzen Artikel lesen …
 Bodendiagonale
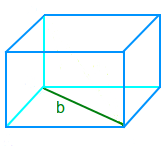
Bodendiagonale
Definition
Eine Diagonale ist eine Linie zwischen zwei Ecken. Es müssen gegenüberliegende Ecken sein. Bodendiagonalen laufen unten auf dem Boden entlang. Hier steht noch etwas zur Berechnung der Bodendiagonale. => Ganzen Artikel lesen …
Durchmesser
D oder d: eine Diagonale geht per Definition immer von einer Ecke zu einer gegenüberlüberliegenden Ecke. Da Kugeln keine Ecken haben, haben Kugeln auch keine Diagonale. Bei Kugeln spricht man vom => Kugeldurchmesser
D
Der Durchmesser: Diagonalen gehen immer von einer Ecke zu einer anderen. Kreise haben keine Ecken, also auch keine Diagonalen. Bei einem Kreis spricht man vom => Kreisdurchmesser
 Nebendiagonale
Nebendiagonale
… von unten links nach oben rechts, siehe auch => Hauptdiagonale
 Kistendiagonale berechnen
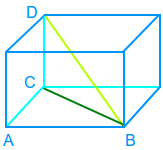
Kistendiagonale berechnen
Formel
d = √(l²+b²+h²) ist die Formel zur Berechnung der Länge einer Raumdiagonalen in einer Kiste. Diese Formel ist hier ausführlich erklärt. => Ganzen Artikel lesen …
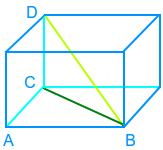 Kistendiagonale über Pythagoras
Kistendiagonale über Pythagoras
Lösungsidee
Von einer rechtwinkligen Kiste, geometrisch ein Quader, soll die Länge der Raumdiagonalen berechnet werden, wenn alle Kantenlängen der Kiste bekannt sind oder leicht gemessen werden können. Über den Satz des Pythagoras berechnet man dann erst die Länge der Bodendiagonalen. Dann kann man sich mit der Bodendiagonalen ein senkrecht stehendes rechtwinkliges Dreieck denken: Die Bodendiagonale ist eine Kathete, die Kistenhöhe die andere und die Hypotenuse ist die gesucht => Kistendiagonale

