Berechnung
Zähler und Nenner vertauschen gibt immer den Kehrwert von einem Bruch. Es gibt nur eine Ausnahme. Das ist hier kurz erklärt. => Ganzen Artikel lesen …
 Kehrwert
Kehrwert
Algebra
Der Kehrwert k einer Zahl a ist diejenige Zahl k, mit der man a multiplizieren muss, sodass am Ende genau 1 herauskommt. Der Kehrwert von 2 ist 0,5 denn: 2·0,5=1. Fast alle Zahlen haben einen Kehrwert. Es gibt nur eine Ausnahme. => Ganzen Artikel lesen …
Mathematik
Von x=4 bis x=7 gibt einen Bereich an. Das Wort von bezeichnet dabei den Anfang. Um eindeutig zu sagen, ob der Anfang oder auch das Ende mit dem zu dem betrachteten Bereich gehören soll, gibt es in der Mathematik speziell dafür entwickelte Schreibweisen. Siehe mehr dazu unter => Intervall
 Bruch
Bruch
z. B. ½
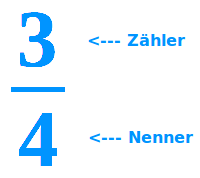
Als Bruch bezeichnet man jede Zahl, die mit einem Bruchstrich in der Form ⅖ oder 3/4 geschrieben ist. Die Zahl links oder oben vom Bruchstrich ist der Zähler, die Zahl rechts oder unten vom Bruchstrich der Nenner. Im engeren Sinn dürfen der Zähler und der Nenner jeweils nur eine ganze Zahl sein dürfen (z. B. -4, 5 oder 111). In einem verallgemeinerten Sinn dürfen Zähler und Nenner jede beliebige Reelle Zahl sein. Lediglich der Nenner (unten) in keinem Fall den Wert Null annehmen. [1] Mehr dazu unter => Bruchzahl
… oben und unten vertauschen, mehr unter => Kehrwert von einem Bruch
… oben und unten vertauschen, mehr unter => Kehrwert von einem Bruch
… einfach Zähler und Nenner vertauschen, mehr unter => Kehrwert von einem Bruch

