Matrizenrechnung
In der Rechnung mit Matrizen steht „die Inverse“ oft als Kurzform für eine sogenannte => Inverse Matrix [1]
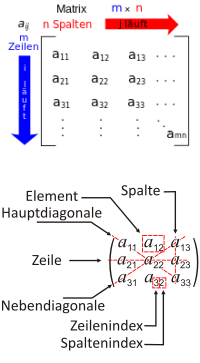 Matrix
Matrix
Mathematik
Kurzdefinition: eine Matrix ist eine tabellartige Anordnung von Elementen, meist von Zahlen. Mit Matrizen kann man dann verschiedene Rechnungen durchführen [1], so als sei die ganze Matrix eine Zahl. => Ganzen Artikel lesen …
 Inverse Matrix
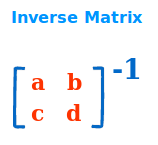
Inverse Matrix
A⁻¹
Ein inverse Matrix, auch Kehrmatrix, Umkehrmatrix oder kurz Inverse ist eine Art Kehrwert in der Matrizenrechnung. Hat man eine Matrix A, dann gibt das Produkt aus A und ihrer Inversen A⁻¹ immer die sogenannte Einheitsmatrix 𝟙, kurz: A·A⁻¹=𝟙. => Ganzen Artikel lesen …
Beispiele
Eine reguläre (Determinante ist nicht 0), quadratische Matrix (Zeilenzahl = Spaltenzahl) kann immer in eine invertierte Matrix umgewandelt werden. Dazu gibt es verschiedene Rechenverfahren, die eher aufwändig sind. Eine Matriz mal ihrer Inversen ergibt immer die Einheitsmatrix. Hier stehen Beispiele. => Ganzen Artikel lesen …
 Drehmatrix
Drehmatrix
Geometrie
In einem 2D-Koordinatensystem, auch als euklidische Ebene ℝ² bezeichnet, kann man einen Ortsvektor mit Hilfe einer Matrix über eine einfache Rechnung um einen gewünschten Winkel α um den Koordinatenursprung (0|0) gegen den Uhrzeigersinn drehen. Man spricht von einer Vektordrehung oder einer Vektorrotation. Die Lösungsidee dazu ist die sogenannte Drehmatrix, oft bezeichnet als R mit einem rechts tiefgestellten kleinen Alpha. Hier ist der Rechenweg in Worten und mit Zahlenbeispielen erklärt. => Ganzen Artikel lesen …
 Einheitsmatrix
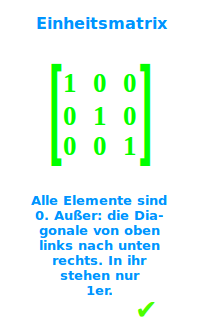
Einheitsmatrix
𝟙
Alle Elemente einer sogenannten Einheitsmatrix sind Nullen. Nur in der Hauptdiagonalen, die Diagonale von oben links nach unten rechts) stehen keine Nullen sondern ausschließlich nur Einsen als Einträge. Die Einheitsmatrix ist damit ein Sonderfall einer Diagonalmatrix. Eine übliche Abkürzung ist der lichte Buchstabe 𝟙, eine 1 mit doppelt geschriebenem senkrechten Strich. => Ganzen Artikel lesen …
Matrizen
Determinante ist 0: [1] der Begriff ist nur für quadratische Matrizen definiert. Eine quadratische Matrix hat genauso viele Spalten wie Zeilen. Eine solche Matrix heißt genau dann singulär, seltener auch entartet [2][4], wenn ihre Determinante den Wert 0 annimmt. Nimmt sie einen von Null verschiedenen Wert an, ist sie eine reguläre Matrix. => Ganzen Artikel lesen …

