… mit u und v oder g(x) und f(Siehe unter => Partielle Integration
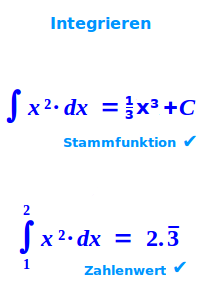Integrieren
Mathematik
Zu f(x) eine Aufleitung F(x) oder den konkreten Zahlenwert für bestimmte Grenzen dafür berechnen: beides wird oft integrieren oder auch aufleiten genannt. Hier steht eine kurze Unterscheidung der zwei Begriffe. => Ganzen Artikel lesen …
Über
Räumlich | Sinnbildlich | Kombinatorik
Von unten aus gesehen weiter oben. Im übertragenen Sinn heißt über auch so viel wie: mit Hilfe von. In der Kombinatorik steht es für einen bestimmten Term mit Fakultäten. Die Fälle sind hier kurz vorgestellt. => Ganzen Artikel lesen …
Mathematik
Das Aufsuchen aller möglichen Stammfunktion F(x) zu einer gegebenen Funktion f(x) nennt man Integration [1]. Beispiel: f(x)=x hat als Stammfunktion zum Beispiel F(x)=½x²+1 oder auch F(x)=½x+9 oder F(x)=½x-22. Jede Funktion F(x), die abgeleitet wieder f(x) gibt eine Stammfunktion F(x) von f(x). Mehr dazu steht im Artikel => integrieren
… siehe unter => Integrieren über partielle Integration
… siehe unter => Integrieren über partielle Integration
… siehe unter => Integrieren über partielle Integration
… Erklärung mit Beispiel unter => Partiell integrieren
