Analysis
Eine Gleichung, bei der die Unbekannte in einem Integralterm enthalten ist, nennt man eine Integralgleichung. Beispiel: Das Integral von f(x)=3x² in den Grenzen von 1 bis b soll genau den Wert 7 ergeben. Das kleine b ist dann die Unbekannte. Man löst den Integralterm dazu auf, setzt ihn gleich 7 und löst nach der Unbekannten auf. Dabei erhält man b=2. Wie man den Integralterm auflöst ist erklärt im Artikel zum => Integralzeichen
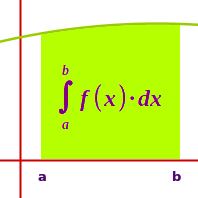Integralrechnung
∫f(x)·dx
Zusammen mit der Differentialrechnung bildet die Integralrechnung das mathematische Teilgebiet der Analysis. Die Integralrechnung im engeren Sinn beschäftigt sich mit Flächenelementen von Graphen. In der Praxis spielt sie eine Rolle, wo die Effekte langfristig sich verändernder Prozesse aufsummiert werden. => Ganzen Artikel lesen …
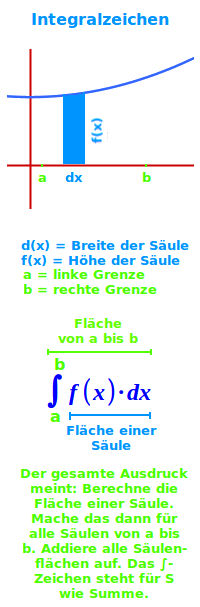Integralzeichen
∫f(x)·dx anschaulich
∫f(x)·dx liest man als: Das Integral von f(x) in den Grenzen von a bis b. Eine Zahl für a steht dabei immer links unten am Integralzeichen und b oben links am Integralzeichen. Es meint: bilde eine Stammfunktion zu f(x). Diese Stammfunktion nennt man dann F(x). Rechne dann F(b)-F(a). Das Ergebnis nennt man das Integral. Das ist hier ausführlich und anschaulich erklärt. => Ganzen Artikel lesen …
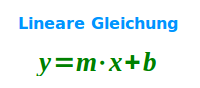Lineare Gleichung
Definition
Jede Gleichung, die man umformen kann in y = m·x+b nennt man linear. Wichtig ist, dass das x keine Hochzahl (außer der gedachten 1) hat und auch nicht in einem Nenner steht. Das ist hier näher erklärt. => Ganzen Artikel lesen …
… Zahl + oder - am Ende einer Aufleitung => Integrationskonstante
